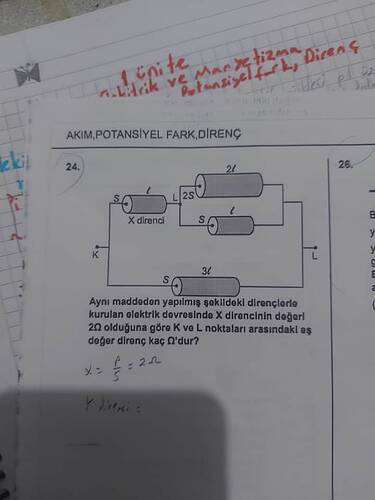
Verilen Devre İçin Eşdeğer Direnç Hesabı
Soru: Aynı maddeden yapılmış şekildeki dirençlerle kurulan elektrik devresinde X direncinin değeri 2\Omega olduğuna göre K ve L noktaları arasındaki eşdeğer direnç kaç \Omega'dur?
Cevap:
Dirençler bir telin uzunluğuna ve kesitine göre şu şekilde hesaplanır:
[ R = \rho \frac{L}{A} ]
Burada \rho telin özdirenci, L uzunluk, A ise kesit alanıdır. Bu durumda özdirenç ve kesit alanı sabit olduğuna göre, direncin uzunlukla doğru orantılı olduğunu söyleyebiliriz.
1. X Direnci
[ X = \rho \frac{l}{A} = 2\Omega ]
2. Diğer Dirençler
-
2S uzunluğundaki direnç (paralel)
[ R_1 = \rho \frac{2l}{A} = 4\Omega ]
-
3L uzunluğundaki direnç
[ R_2 = \rho \frac{3l}{A} = 6\Omega ]
3. Paralel Dirençler
2L ve 2S uzunluğundaki dirençler paraleldir:
[ \frac{1}{R_{\text{paralel}}} = \frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2} ]
[ R_{\text{paralel}} = 2\Omega ]
4. Toplam Eşdeğer Direnç
K ve L noktaları arasındaki eşdeğer direnç, X direnci ve 3L uzunluğundaki dirençle birlikte seri bağlıdır:
[ R_{\text{eşdeğer}} = R_{\text{paralel}} + R_2 ]
[ R_{\text{eşdeğer}} = 2\Omega + 6\Omega ]
[ R_{\text{eşdeğer}} = 8\Omega ]
Sonuç: K ve L noktaları arasındaki eşdeğer direnç 8 \Omega'dur.
Özet: Paralel ve seri bağlantıların nasıl çalıştığını, ve direncin uzunluğa olan bağımlılığını kullanarak K ve L noktaları arasındaki eşdeğer direnci hesapladık.