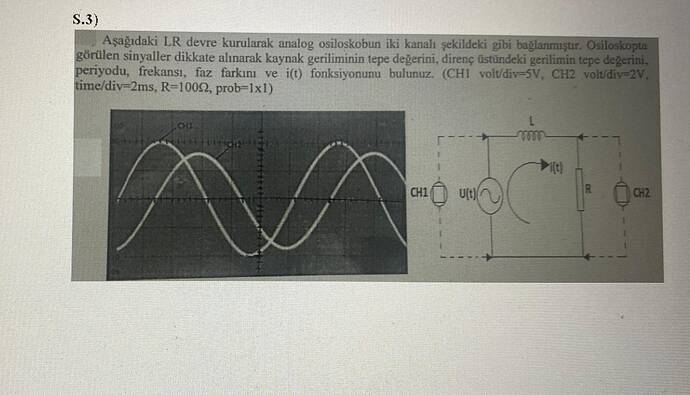
Verilen Soru
Cevap:
Bu soruda, bir LR devresi üzerinden osiloskopta görüntülenen sinyaller dikkate alınarak çeşitli elektriksel büyüklüklerin hesaplanması isteniyor. Aşağıda bu adımları tek tek ele alarak çözümü yapacağız.
Adım 1: Gözlemler ve İlk Bilgilendirmeler
-
Osiloskop Ayarları:
- CH1: Volt/div = 5V
- CH2: Volt/div = 2V
- Time/div = 2ms
-
Direnç (R): 100Ω
Osiloskop ekranında verilen sinüzoidal dalga şekli dikkatle incelendiğinde, tepe değerlerini, periyodu ve faz farkını bulmaya başlayabiliriz.
Adım 2: Tepe Değerleri
-
Kaynak Geriliminin Tepe Değeri (CH1):
- CH1’deki dalganın tepe değeri yaklaşık 3 bölme.
- Tepe gerilimi: (3 \times 5V = 15V).
-
Direnç Üzerindeki Gerilimin Tepe Değeri (CH2):
- CH2’deki dalganın tepe değeri yaklaşık 2.5 bölme.
- Tepe gerilimi: (2.5 \times 2V = 5V).
Adım 3: Periyot ve Frekans Hesabı
-
Periyot: Bir tam dalga 4 bölmeyi kaplıyor.
- Periyot (T = 4 \times 2\text{ms} = 8\text{ms}).
-
Frekans: Frekans (f = \frac{1}{T} = \frac{1}{8\text{ms}} = 125\text{Hz}).
Adım 4: Faz Farkı
Faz farkını hesaplamak için, iki sinüs dalgası arasındaki yatay farkı ölçüyoruz.
- Görülen fark yaklaşık yarım bölme.
- Faz farkı: (\Delta t = 0.5 \times 2\text{ms} = 1\text{ms}).
- Faz farkı: (\Delta \phi = \frac{\Delta t}{T} \times 360^\circ = \frac{1\text{ms}}{8\text{ms}} \times 360^\circ = 45^\circ).
Adım 5: Akım Fonksiyonunun i(t) Bulunması
Verilen direnç ve üzerinde ölçülen gerilim ile akım hesabı yapılabilir.
- Tepe akımı (I_m = \frac{5V}{100\Omega} = 0.05A).
i(t) fonksiyonu ise:
$$i(t) = I_m \cos(2\pi ft + \Delta \phi) = 0.05 \cos(2\pi \times 125t + 45^\circ)$$
Nihai Cevap
- Kaynak Geriliminin Tepe Değeri: 15V
- Direnç Üzerindeki Gerilimin Tepe Değeri: 5V
- Periyot: 8ms
- Frekans: 125Hz
- Faz Farkı: 45 derece
- i(t) Fonksiyonu: (0.05 \cos(2\pi \times 125t + 45^\circ))
Bu tür sinüzoidal dalga analizleri osiloskop kullanımını güçlendirir ve devre analizi yeteneklerini artırır.