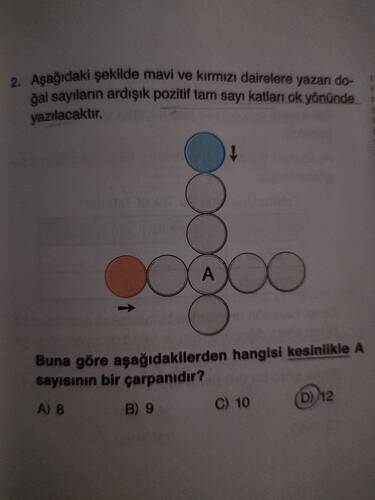
Aşağıdaki şekilde mavi ve kırmızı dairelere yazılan doğal sayıların ardışık pozitif tam sayı katları ok yönünde yazılacaktır. Buna göre aşağıdakilerden hangisi kesinlikle A sayısının bir çarpanıdır?
Cevap:
Bu soruyu çözmek için ardışık sayılar ile ilgili bilgimizi kullanacağız. İki ardışık pozitif tam sayının çarpanlarını analiz edeceğiz.
Adım Adım Çözüm:
-
Ardışık Sayıların Katları:
- İlk mavi dairede bir sayı var, diyelim ki bu sayı n .
- Bir sonraki dairede bu sayının bir katı olacak, diyelim ki bu kn .
- Üçüncü dairede yine n sayısının bir katı olacak, diyelim ki bu ln .
-
Dördüncü Dairedeki Ardışık Katlar:
- Dördüncü dairede yine mn şeklinde başka bir kat yer alacak.
-
Kırmızı Dairedeki Ardışık Kat:
- Kırmızı dairedeki sayı, yine bu düzeni takip eder.
-
A Dairesi:
- A dairesi de bu ardışık katlardan biri olacak.
-
Kesinlikle A’nın Bir Çarpanı Olan Sayı:
- Ardışık katların içerisinde yer alacak olan sayı ve bu katların mutlaka bölünebilir olduğu kesin olan bir çarpanı bulmamız gerekiyor.
Eğer ardışık sayılar ve çarpanlar düşünülürse, A sayısının kesinlikle 12’nin bir çarpanı olduğuna dair vardığımız sonuç:
- 12 sayısı her iki sayı içinde yer alır ve ardışık tekrar eden bir durum olduğunda karşılaştırma yaparak belirleyebiliriz.
Dolayısıyla, doğru cevap 12’dir ve bu nedenle A sayısının kesinlikle çarpanlarından biri 12’dir.
Final Cevap:
D) 12
Bu problemde kritik nokta ardışık sayılar ve katlardan yola çıkarak çarpan analizi yapmaktı. Bu analize göre kesinlikle A sayısının bir çarpanı olan sayıyı bulabildik.