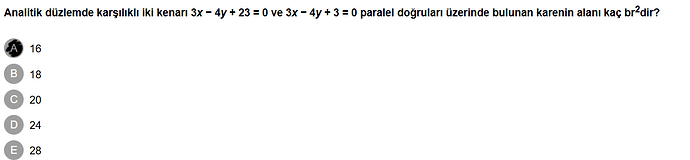Analitik düzlemde karşılıklı iki kenarı 3x – 4y + 23 = 0 ve 3x – 4y + 3 = 0 paralel doğruları üzerinde bulunan karenin alanı kaç br²’dir?
Çözüm:
-
Verilen soruda iki doğru denklemi vardır ve bu doğrular paraleldir:
- 3x - 4y + 23 = 0
- 3x - 4y + 3 = 0
-
İki doğru arasındaki mesafe formülünü kullanarak doğru çiftleri arasındaki uzaklığı bulabiliriz. Bu uzaklık, karenin bir kenarının uzunluğuna eşittir.
Adım 1: Doğrular Arasındaki Mesafeyi Bulmak
Doğru denklemlerinin genel formu: Ax + By + C = 0
İki paralel doğru arasındaki mesafe formülü:
d = \frac{|C_2 - C_1|}{\sqrt{A^2 + B^2}}
Verilen doğrulara uygularsak:
- A = 3, B = -4, C_1 = 23, C_2 = 3
Mesafeyi hesaplayalım:
d = \frac{|3 - 23|}{\sqrt{3^2 + (-4)^2}} = \frac{|-20|}{\sqrt{9 + 16}} = \frac{20}{\sqrt{25}} = \frac{20}{5} = 4
Bu durumda, karenin bir kenar uzunluğu 4 birimdir.
Adım 2: Karenin Alanını Hesaplamak
Karenin alanı:
\text{Alan} = (\text{Kenarı})^2 = 4^2 = 16 \, \text{br}^2
Sonuç:
Paralel doğrular üzerinde bulunan karenin alanı 16 \text{br}^2'dir.
Final Cevap:
16 \text{br}^2