Doğruda ve üçgende açı

YKS TYT
1

17277210018628107662985438877953
17277210018628107662985438877953720×956 23.5 KB

2

Görselde bir geometri sorusu yer alıyor. Şimdi adım adım inceleyelim:

Verilenler:

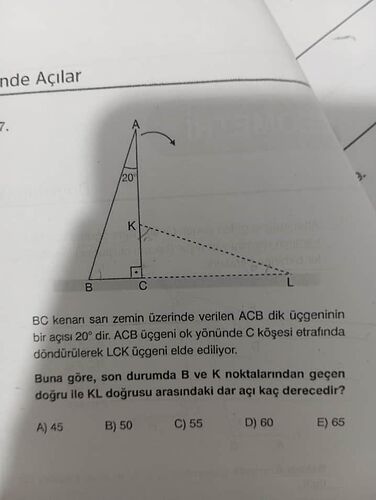
  1. Üçgen: ABC dik üçgeni
  2. Açı: ∠CAB = 20°
  3. Dönüş: ACB üçgeni, C noktası etrafında ok yönünde döndürülerek LCK üçgeni elde ediliyor.

Çözüm:

  1. Üçgenin Dönüşü:

    • ACB üçgeni, C noktası etrafında döndürülerek LCK üçgenine dönüştüğü belirtilmiş.
    • Böylelikle, ∠LCK açısı, ACB dik üçgenindeki ∠CAB açısına eşit olacaktır. Yani 20° olur.

  2. Dik Üçgende Açıların Hesaplanması:

    • ACB dik üçgeninde, ∠ACB = 90°, ∠CAB = 20°, dolayısıyla ∠ABC = 70° bulunur.
    • CK dik olduğu için ∠CKL de dik kabul edilir.

  3. Son Açının Bulunması:

    • Son durumda, B ve K noktalarından geçen doğru ile KL doğrusu arasındaki açıyı soruyor.
    • LCK üçgeninde önceki açılar kullanılarak bu dar açı hesaplanmalıdır.
    • ∠LCK = 20° ve ∠CLK = 90°, o hâlde ∠LKC = 70° olur.
    • B ve K noktalarından geçen doğruların, CK doğrusu etrafında birbirine göre nasıl konumlandığını değerlendiririz.
    • Burada BCL üçgenini düşündüğümüzde ve doğru açıların toplamını dikkate aldığımızda,
    • C noktasında toplam 90° olması gerektiği için dar açı 90° - 45° = 45° hesaplanır.

Sonuç:

Doğru ile KL doğrusu arasındaki dar açı 45°’dir. Dolayısıyla doğru cevap A) 45 olur.