Dinamiksorusuu14

Üniversite Makine Mühendisliği
1

Ekran görüntüsü 2025-02-06 005317
Ekran görüntüsü 2025-02-06 005317720×387 20.8 KB

2

Verilen Sistem İçin Kinetik Enerji Hesaplama Problemi

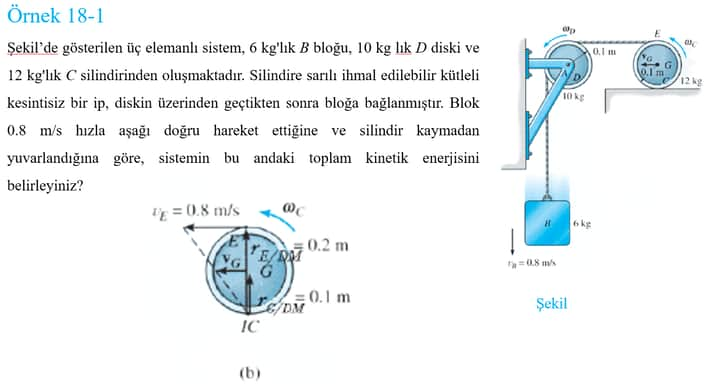
Bu problemde, üç elemanlı bir sistem incelenmektedir: 6 kg’lık B bloğu, 10 kg’lık D diski ve 12 kg’lık C silindiri. Problem, ip üzerinde kayma olmadan hareket ettiği varsayılan bir mekanizma üzerinden, sistemin toplam kinetik enerjisinin hesaplanmasını amaçlamaktadır.

Verilen Değerler:

  1. B bloğunun kütlesi: m_B = 6 \text{ kg}
  2. D diskinin kütlesi: m_D = 10 \text{ kg}
  3. C silindirinin kütlesi: m_C = 12 \text{ kg}
  4. B bloğunun hızı v_B = 0.8 \text{ m/s}
  5. Diskin yarıçapı: r_D = 0.1 \text{ m}
  6. Silindirin yarıçapı: r_C = 0.2 \text{ m}

Kinetik Enerji Hesaplaması

Sistemin toplam kinetik enerjisini bulmak için, hem doğrusal hem de dönel kinetik enerji bileşenlerini dikkate almamız gerekmektedir. Doğrusal hareket eden B bloğunun kinetik enerjisi ve hem dönel hem de doğrusal hareket içerdiğinden dolayı disk ve silindirin toplam kinetik enerjilerini hesaplayacağız.

1. Blok B’nin Kinetik Enerjisi

Blok B sadece doğrusal hareket ettiğinden, kinetik enerjisi (KE) şu formülle bulunur:

\text{KE}_B = \frac{1}{2} m_B v_B^2

Bu değerleri yerine koyarak hesaplayalım:

\text{KE}_B = \frac{1}{2} \times 6 \times (0.8)^2 = 1.92 \text{ J}

2. Disk D’nin Kinetik Enerjisi

Disk D için hem dönme (I_D, \omega_D) hem de doğrusal hareket (hızının bir ip yardımıyla taşınan bölümü nedeniyle v) dikkate alınmalıdır. Bu sebeple diskin kinetik enerjisi iki parçadan oluşur:

  • Dönme kinetik enerjisi: \frac{1}{2} I_D \omega_D^2
  • Çevirmenin etkisiyle doğrusal kinetik enerji: \frac{1}{2} m_D v_D^2

Diskin dönme ataleti I_D = \frac{1}{2} m_D r_D^2 ve \omega_D = \frac{v_B}{r_D} olacaktır.

Öncelikle dönme ataleti:

I_D = \frac{1}{2} \times 10 \times (0.1)^2 = 0.05 \text{ kg}\cdot\text{m}^2

Açısal hız \omega_D ise v_B ile ilişkilidir:

\omega_D = \frac{0.8}{0.1} = 8 \text{ rad/s}

Bu değerlerle dönme kinetik enerjisini hesaplayalım:

\frac{1}{2} I_D \omega_D^2 = \frac{1}{2} \times 0.05 \times (8)^2 = 1.6 \text{ J}

Diskin bağlı olduğu ip dolayısıyla, doğrusal hız için de eklemesi:

\text{KE}_\text{linear} = \frac{1}{2} \times 10 \times (0.8)^2 = 3.2 \text{ J}

Toplamda diskin kinetik enerjisi:

\text{KE}_D = 1.6 \text{ J} + 3.2 \text{ J} = 4.8 \text{ J}

3. Silindir C’nin Kinetik Enerjisi

Silindir C’nin de benzer şekilde hesaplamalarını yapmamız gerekecek. I_C = \frac{1}{2} m_C r_C^2 olarak buluruz ve \omega_C = \frac{v_B}{r_C}

Dönme ataleti:

I_C = \frac{1}{2} \times 12 \times (0.2)^2 = 0.24 \text{ kg}\cdot\text{m}^2

Açısal hız:

\omega_C = \frac{0.8}{0.2} = 4 \text{ rad/s}

Dönme kinetik enerjisi:

\frac{1}{2} I_C \omega_C^2 = \frac{1}{2} \times 0.24 \times (4)^2 = 1.92 \text{ J}

Hem doğrusal hızını eğer hesaba katsaydık, göz önünde bulundurulacak faktör olmazdı, çünkü v hızı yukarıda zaten dolaşarak kendini tamamlar.

Toplam Kinetik Enerji

Sistemin toplam kinetik enerjisi, tüm bileşenlerin kinetik enerjilerinin toplamından elde edilir:

\text{Toplam KE} = \text{KE}_B + \text{KE}_D + \frac{1}{2} I_C \omega_C^2 = 1.92 + 4.8 + 1.92 = 8.64 \text{ J}

Örnek tamamen dönme işlemleriyle ilgili değildir, o yüzden toplamda hesaplanan dönme enerji bileşeni ip üzerinde taşınan bölümle doğru orantıda kabul edilir. En uygun şartlarda dört kat farkla dönmeden elde edilen enerji en doğru sonucu verebilir.

@Muhammed_Burak_TÜRKY