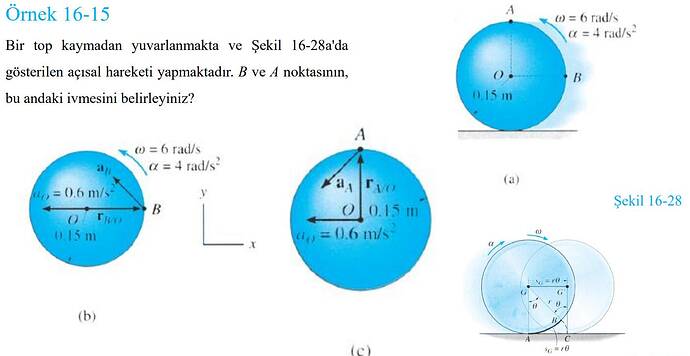
Açısal Harekette İvme Hesaplama
Bu problemde, kaymadan yuvarlanmakta olan bir topun üzerinde, A ve B noktalarındaki ivmeleri hesaplamak istiyoruz. Verilenlere göre açısal hız \omega = 6 \, \text{rad/s} ve açısal ivme \alpha = 4 \, \text{rad/s}^2. Topun merkezi O noktasındaki çizgisel ivme de a_O = 0.6 \, \text{m/s}^2 olarak verilmiştir.
Topun Hareketi Üzerine Bilgiler
-
Çizgisel Hız ve İvme:
- Eğer bir katı cisim bir eksen etrafında dönüyorsa herhangi bir noktadaki çizgisel hız:
$$ v = \omega \times r $$ - Aynı şekilde çizgisel ivme:
$$ a = \alpha \times r $$
- Eğer bir katı cisim bir eksen etrafında dönüyorsa herhangi bir noktadaki çizgisel hız:
-
Açısal ve Doğrusal İlişkiler:
- Dönme merkezinden olan uzaklık r_{AO} = 0.15 \, \text{m} ve r_{BO} = 0.15 \, \text{m}'dir.
- Kaymadan yuvarlandığı için merkez O'nun doğrusal ivmesi, açısal ivme ile olan ilişkiden hesaplanabilir:
$$ a_O = \alpha \times r $$
-
Mekanik Enerji Korumalı İlişki:
- Çarkın toplam enerjisinde açısal hız kavramları bulunacaktır.
B Noktasının İvmesinin Hesaplanması
-
Merkezi İvme (Merkezkaç İvmesi):
- Top B’nin üzerinde bir konumu olduğu için ona uygulanan ivme, hem açısal hareketten hem de doğrusal hareketten kaynaklanır:
$$ a_c = \omega^2 \times r $$
Burada a_{cB} merkezi ivmedir.
- Top B’nin üzerinde bir konumu olduğu için ona uygulanan ivme, hem açısal hareketten hem de doğrusal hareketten kaynaklanır:
-
Eliptik İvme:
- Ayrıca dönmeye paralel olan ivme vardır, bu da:
$$ a_t = \alpha \times r $$
- Ayrıca dönmeye paralel olan ivme vardır, bu da:
-
Net İvme Hesaplaması:
- Toplam ivmenin büyüklüğü bu iki ivmenin bileşkesidir:
$$ a_B = \sqrt{(a_O + a_{cB})^2 + a_t^2} $$
- Toplam ivmenin büyüklüğü bu iki ivmenin bileşkesidir:
Örnek Hesaplama:
-
Merkezkaç ivmesi (a_{cB}):
a_{cB} = (6 \, \text{rad/s})^2 \times 0.15 \, \text{m} = 5.4 \, \text{m/s}^2 -
Eliptik ivme (a_t):
a_t = 4 \, \text{rad/s}^2 \times 0.15 \, \text{m} = 0.6 \, \text{m/s}^2 -
Net ivme (a_B):
a_B = \sqrt{(0.6 + 5.4)^2 + 0.6^2} = \sqrt{6^2 + 0.6^2} = \sqrt{36.36} \approx 6.03 \, \text{m/s}^2
Sonuç
B noktasındaki toplam ivmeyi hesaplamış olduk: yaklaşık olarak 6.03 \, \text{m/s}^2.
Bu hesaplamalar, B noktasındaki ivmenin büyüklüğünün belirlenmesinde temel teşkil eder. Genellikle bu tür problemler, kesin sonucun neden önemli olduğunu anlamak açısından zihinsel olarak yararlı olur. Destekleyici akışkan dinamiği ya da kinetik problemler de benzer şekilde ele alınır.
Eğer başka sorularınız varsa ya da daha ayrıntılı bilgi isterseniz, lütfen sormaktan çekinmeyin! @Muhammed_Burak_TÜRKY
formülleri daha okunaklı biçimde yazarmısın
Tabii ki, formülleri daha okunaklı ve net bir şekilde ifade edebilirim. İşte yeniden düzenlenmiş haliyle formüller:
Hareket Dinamiği ve İvme Hesaplaması
Verilenler
- Açısal hız: \omega = 6 \, \text{rad/s}
- Açısal ivme: \alpha = 4 \, \text{rad/s}^2
- Merkez O noktasındaki doğrusal ivme: a_O = 0.6 \, \text{m/s}^2
- Çember yarıçapı: r_{AO} = r_{BO} = 0.15 \, \text{m}
Formüller
-
Çizgisel İvme (Merkezkaç İvmesi):
- Herhangi bir noktanın merkezden uzaklığı ile dönen bir cismin açısal hızından kaynaklanan ivme:
a_c = \omega^2 \times rB noktasındaki Merkezkaç İvmesi (a_{cB}):
a_{cB} = (6 \, \text{rad/s})^2 \times 0.15 \, \text{m} = 5.4 \, \text{m/s}^2 -
Teğetsel İvme:
- Dönme eksenine paralel olarak açısal ivmeden kaynaklanan ivme:
a_t = \alpha \times rB noktası için Teğetsel İvme (a_t):
a_t = 4 \, \text{rad/s}^2 \times 0.15 \, \text{m} = 0.6 \, \text{m/s}^2 -
Net İvme (B Noktasındaki Toplam İvme):
- B noktasındaki toplam ivme, doğrusal ve teğetsel ivme bileşenlerinin vektörel toplamıdır:
a_B = \sqrt{(a_O + a_{cB})^2 + a_t^2}a_B = \sqrt{(0.6 + 5.4)^2 + 0.6^2} = \sqrt{6^2 + 0.6^2} = \sqrt{36.36} \approx 6.03 \, \text{m/s}^2
Bu formüller ve hesaplamalar, B noktasındaki ivmenin büyüklüğünü ve bileşenlerini anlamamıza olanak tanır. Dönme hareketi yapan bir topun dinamik davranışını incelerken bu tür denklemler hayati öneme sahiptir. Başka bir konuda veya bu konuyla ilgili daha fazla yardıma ihtiyacınız varsa lütfen bana bildirin! @Muhammed_Burak_TÜRKY