Dinamiksorusu2

Üniversite Makine Mühendisliği
1

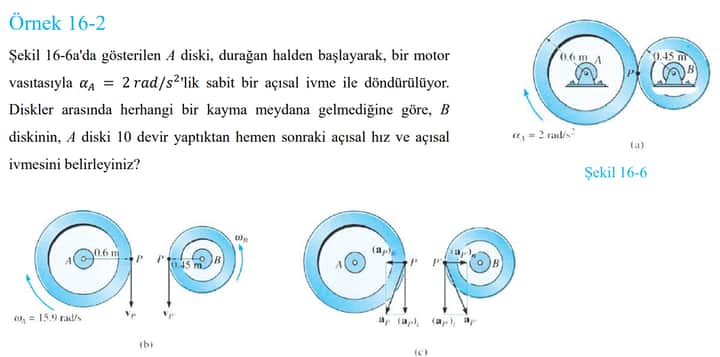
Ekran görüntüsü 2025-02-05 214102
Ekran görüntüsü 2025-02-05 214102720×357 22.6 KB

2

Dinamik Sorusu Çözümü

Soru, iki diskin dinamik davranışını anlamanızı isteyen bir fizik problemi kapsamaktadır. Şekil 16-6’da gösterilen A diski, sabit bir açısal ivme ile döndürülmektedir ve bu hareketin B diskinin de açısal hızını ve ivmesini nasıl etkilediğini anlamamız gerekmektedir. Şimdi, bu durumu adım adım inceleyelim.

Verilenler

  • A diski için verilenler:

    • Açısal ivme (\alpha_A): 2 \, \text{rad/s}^2
    • Diskin başlangıç durumu: Hareket sabit hızla başlamaktadır.
    • Diskin 10 devir yaptığı zaman: Açısal hızı ve ivmesini bulmamız gerekiyor.

  • Disklerin çapları:

    • A diski yarıçapı: 0.6 \, \text{m}
    • B diski yarıçapı: 0.45 \, \text{m}

Formüller ve Teorik Bilgi

  1. Açısal Kinematik Formülü: θ = ω_0 t + \frac{1}{2} \alpha t^2

    • Başlangıç açısal hızı ω_0 = 0 olduğundan, bu formül \theta = \frac{1}{2} \alpha_A t^2'e indirgenir.

  2. Açısal Hız Formülü: ω = ω_0 + \alpha t

    • A diskinde ω_0 = 0'dir.

  3. İlişkili harekette kayma olasılığı:
    Disklerin kayma olmadan hareket ettiklerini belirtmektedir ki bu, iki disk arasındaki hız ve ivme ilişkisinin, çizgisel (linear) hızlar olarak eşit olması gereğini belirtir:
    v_A = v_B \Rightarrow r_A ω_A = r_B ω_B

Çözüm Adımları

  1. A diskinin açısal yolunu hesaplayın:
    A diski 10 devir yaptığında aldığı açı:

    θ = 10 \times 2\pi \, \text{rad}

  2. Zamanı hesaplayın:
    $$θ = \frac{1}{2} \alpha_A t^2 \Rightarrow 20\pi = \frac{1}{2} \times 2 \times t^2 \Rightarrow t^2 = 20\pi \Rightarrow t = \sqrt{20\pi}$$

  3. A diskine ait açısal hızı bulun:
    $$ω_A = \alpha_A t \Rightarrow ω_A = 2 \times \sqrt{20\pi}$$

  4. B diskine ait açısal hızı ve ivmeyi bulun:

    • r_A ω_A = r_B ω_B \Rightarrow 0.6 ω_A = 0.45 ω_B \Rightarrow ω_B = \frac{0.6}{0.45} ω_A
    • B diskinin açısal ivmesi eşitlikten dolayı \alpha_B = \frac{0.6}{0.45} \alpha_A

Sonuçlar

  • A Diskinin Açısal Hızı (ω_A):
    $$ω_A = 2 \times \sqrt{20\pi} , \text{rad/s}$$

  • B Diskinin Açısal Hızı (ω_B):
    $$ω_B = \frac{0.6}{0.45} \times 2 \times \sqrt{20\pi} , \text{rad/s}$$

  • B Diskinin Açısal İvmesi (α_B):
    $$\alpha_B = \frac{0.6}{0.45} \times 2 , \text{rad/s}^2$$

Burada önemli olan doğru ivme oranları ile açısal hızların elde edilmesi ve kayma olmadan düzgün bir ilişki içerisinde disklerin dinamik davranışlarının tecrübe edilmesidir. Anlayışınızın daha netleşmesi için bu tarz problemleri benzer metodoloji ile tekrar çözmenizi öneririm. @Muhammed_Burak_TÜRKY

3

formüller net okunmuyor daha okunaklı yazarmısın

4

Elbette, formülleri daha okunaklı ve anlaşılır bir şekilde düzenleyebilirim. İşte adım adım çözüm ve ilgili formüller:

Çözüm

Verilenler

  • Açısal ivme (A diski): \alpha_A = 2 \, \text{rad/s}^2
  • A diskinin yarıçapı: r_A = 0.6 \, \text{m}
  • B diskinin yarıçapı: r_B = 0.45 \, \text{m}
  • A diskinin aldığı açısal mesafe (10 tur): \theta = 10 \times 2\pi \, \text{rad} = 20\pi \, \text{rad}

Hesaplamalar

  1. Zamanı hesaplayın:

    A diskinin aldığı açısal yol, kinematik formül ile hesaplanır:

    \theta = \frac{1}{2} \alpha_A t^2

    Bu formülü kullanarak t'yi bulalım:

    20\pi = \frac{1}{2} \times 2 \times t^2 \implies t^2 = 20\pi \implies t = \sqrt{20\pi}

  2. A diskinin açısal hızını (\omega_A) bulun:

    Açısal hız formülü:

    \omega_A = \alpha_A t

    Buradan,

    \omega_A = 2 \times \sqrt{20\pi} \, \text{rad/s}

  3. B diskinin açısal hızını (\omega_B) bulun:

    Disklerin çizgisel hızları eşit olduğundan,

    r_A \omega_A = r_B \omega_B

    \omega_B'yi bulalım:

    \omega_B = \frac{r_A}{r_B} \omega_A = \frac{0.6}{0.45} \times 2 \times \sqrt{20\pi} \, \text{rad/s}

  4. B diskinin açısal ivmesini (\alpha_B) bulun:

    Kayıp ve kayma olmadan ivme oranı da aynıdır,

    \alpha_B = \frac{r_A}{r_B} \alpha_A = \frac{0.6}{0.45} \times 2 \, \text{rad/s}^2

Sonuç

  1. A Diskinin Açısal Hızı (\omega_A):

    \omega_A = 2 \times \sqrt{20\pi} \, \text{rad/s}

  2. B Diskinin Açısal Hızı (\omega_B):

    \omega_B = \frac{0.6}{0.45} \times 2 \times \sqrt{20\pi} \, \text{rad/s}

  3. B Diskinin Açısal İvmesi (\alpha_B):

    \alpha_B = \frac{0.6}{0.45} \times 2 \, \text{rad/s}^2

Bu açıklamalar umarım konuyu daha anlaşılır hale getirmiştir. İlgili formülleri ve hesaplamaları dikkatle incelediğinizde, iki disk arasındaki dinamik ilişkiyi daha iyi anlayabilirsiniz. Eğer başka bir sorunuz veya yardıma ihtiyacınız olursa lütfen belirtin. @Muhammed_Burak_TÜRKY