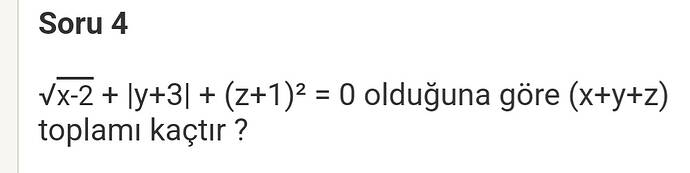Verilen Denklemi İnceleme ve Çözümleme
Verilen denklem:
Bu denklemin sağ tarafı 0 olduğuna göre, her terimin de kendi içinde sıfır olması gerekir, çünkü kök, mutlak değer ve karesel ifade her zaman sıfır veya pozitif değer alır.
Kare Kök İfadesi
-
$$\sqrt{x-2} = 0$$ ifadesini incelediğimizde kök içindeki sayının 0 olması gerektiğini görürüz. Dolayısıyla:
$$x - 2 = 0$$
Buradan, $$x = 2$$ sonucunu elde ederiz.
Mutlak Değer İfadesi
-
$$|y+3| = 0$$ ifadesi için mutlak değerin sıfır veya pozitif olmasından dolayı içerideki ifadenin 0 olması gerekir:
$$y + 3 = 0$$
Buradan, $$y = -3$$ sonucunu elde ederiz.
Karesel İfade
-
$$(z+1)^2 = 0$$ ifadesi için de karesel ifadenin sıfır olması gerektiğinden:
$$z + 1 = 0$$
Buradan, $$z = -1$$ sonucunu elde ederiz.
Sonuçların Toplamı
Artık konumlanan değerlerle (x), (y) ve (z)'yi bulduk. Şimdi (x + y + z) toplamını hesaplayabiliriz:
Sonuç
Bu durumda, (x + y + z) toplamı (-2) olarak bulunur.
Özet olarak, verilen denklemin her terimi ayrı ayrı sıfıra eşitlenerek tek tek çözülmüştür ve toplam sonucumuz (-2) çıkmıştır.