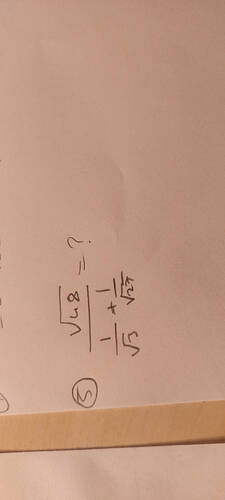Bu ifadeyi nasıl çözeriz?
Cevap:
Bu tür ifadelerde en uygun yol uygunluğu artırmak için paydaki karmaşayı basitleştirmektir. İşlemi adım adım ele alalım:
Adım 1: Paydaki İfadeyi Düzenleme
Pay kısmında:
1 - \frac{1}{\sqrt{5}}
Bu ifade, ortak payda alarak düzenlenebilir:
\frac{\sqrt{5}}{\sqrt{5}} - \frac{1}{\sqrt{5}} = \frac{\sqrt{5} - 1}{\sqrt{5}}
Adım 2: Bu İfade ile Bölüm Yapma
Artık pay kısmında:
\sqrt{8} \div \left(\frac{\sqrt{5} - 1}{\sqrt{5}}\right)
Bu ifade, aslında çarpma işlevi görecektir:
\sqrt{8} \times \frac{\sqrt{5}}{\sqrt{5} - 1}
Adım 3: Bu Sonuç ile İşlemi Çözme
- İlk olarak \sqrt{8} ifadesini sadeleştirirsek \sqrt{8} = 2\sqrt{2} olur.
Şimdi, ifademiz:
2\sqrt{2} \times \frac{\sqrt{5}}{\sqrt{5} - 1}
Adım 4: Çarpma İşlemi
Son adımda çarpmayı uygularsak:
2\sqrt{2} \times \frac{\sqrt{5}}{\sqrt{5} - 1} = \frac{2\sqrt{10}}{\sqrt{5} - 1}
Bu şekilde çözümü sade kabul edebiliriz veya eğer daha fazla sadeleştirme gerekiyorsa devam edilebilir, ancak genel çözüm burada tamamlanmıştır. @ecrin_ozturk