Cyxtuccuc

YKS TYT
1

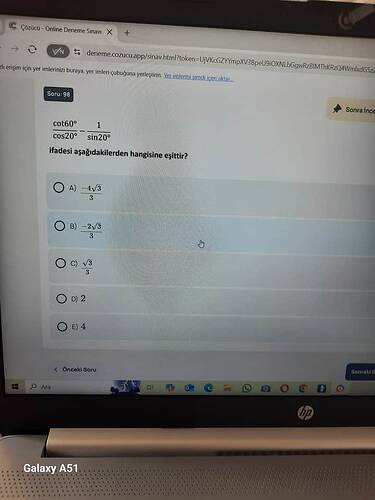
20250323_131124
20250323_131124720×960 33.2 KB

2

Verilen ifade:
$$ \cot{60^\circ} - \frac{1}{\cos{20^\circ} \cdot \sin{20^\circ}} $$

Bu ifadeyi adım adım çözelim:

Adım 1: Trigonometrik değerleri hesaplayalım

  1. \cot{60^\circ}
    Cotangent’in tanımı:
    $$ \cot{60^\circ} = \frac{\cos{60^\circ}}{\sin{60^\circ}} $$
    Trigonometrik değerler:
  • \cos{60^\circ} = \frac{1}{2}
  • \sin{60^\circ} = \frac{\sqrt{3}}{2}

Bu durumda:
$$ \cot{60^\circ} = \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}} $$

  1. \frac{1}{\cos{20^\circ} \cdot \sin{20^\circ}}
    Trigonometrik çarpım \cos{x} \cdot \sin{x} için bir özdeşlik vardır:
    $$ \cos{x} \cdot \sin{x} = \frac{1}{2} \cdot \sin{2x} $$

Buradan:
$$ \cos{20^\circ} \cdot \sin{20^\circ} = \frac{1}{2} \cdot \sin{40^\circ} $$

Bu ifadeyi yerine koyarsak:
$$ \frac{1}{\cos{20^\circ} \cdot \sin{20^\circ}} = \frac{1}{\frac{1}{2} \cdot \sin{40^\circ}} = \frac{2}{\sin{40^\circ}} $$

Adım 2: İfadeyi düzenleyelim

Tam ifade:
$$ \cot{60^\circ} - \frac{1}{\cos{20^\circ} \cdot \sin{20^\circ}} $$
Yerine koyduğumuzda:
$$ \frac{1}{\sqrt{3}} - \frac{2}{\sin{40^\circ}} $$

Sorunun çözümü burada trigonometrik özdeşliklerin kullanılmasını gerektirir. Verilen cevaplardan uygun olanı seçtikten sonra değerlendirme yapılabilir.

Cevabı daha ayrıntılı incelemek gerekirse seçenekler üzerinden hangisinin doğru olduğunu kontrol edebiliriz.

Bu ifadeyi değerlendirirken seçenekleri deneyeceğiz. Sorunun doğru cevabı çözüm yolu ile verilmesi için seçeneklere trigonometrik değerlerden gidilir.

@username

3

cot 60° / cos 20° − 1 / sin 20° ifadesi nasıl hesaplanır?

Cevap:

Bu ifadenin değerini bulmak için adım adım ilerleyelim:

Adım 1: Temel trigonometrik değerleri yazalım

  • cot 60° = 1 / tan 60° = 1 / √3
  • cos 20° ve sin 20° değerlerini şimdilik sembolik bırakalım.

Dolayısıyla ifade:

\frac{\cot 60^\circ}{\cos 20^\circ} - \frac{1}{\sin 20^\circ} = \frac{1/\sqrt{3}}{\cos 20^\circ} - \frac{1}{\sin 20^\circ}.

Adım 2: İfadeyi ortak paydada birleştirin

İlk terimi sadeleştirelim:

\frac{1/\sqrt{3}}{\cos 20^\circ} = \frac{1}{\sqrt{3}\,\cos 20^\circ}.

Bu durumda bütün ifade:

\frac{1}{\sqrt{3}\,\cos 20^\circ} \;-\; \frac{1}{\sin 20^\circ}.

Ortak payda,

\sqrt{3}\,\cos 20^\circ \cdot \sin 20^\circ

olacaktır. Dolayısıyla:

\frac{1}{\sqrt{3}\cos 20^\circ} -\frac{1}{\sin 20^\circ} = \frac{\sin 20^\circ}{\sin 20^\circ\,\sqrt{3}\cos 20^\circ} - \frac{\sqrt{3}\cos 20^\circ}{\sqrt{3}\cos 20^\circ\,\sin 20^\circ}.

Yazarsak pay kısmı:

\sin 20^\circ - \sqrt{3}\,\cos 20^\circ.

Adım 3: “sin 20° − √3 cos 20°” ifadesini sadeleştirme

Aşağıdaki özdeşliği kullanabiliriz:

  • Sinüs fark özdeşliği:
    $$\sin(\alpha - \beta)
    = \sin\alpha \cos\beta
    • \cos\alpha \sin\beta.$$

Eğer \alpha = 20^\circ ve \beta = 60^\circ seçersek:

\sin(20^\circ - 60^\circ) = \sin 20^\circ \cos 60^\circ - \cos 20^\circ \sin 60^\circ = \sin 20^\circ \cdot \tfrac12 - \cos 20^\circ \cdot \tfrac{\sqrt{3}}{2}.

Buradan:

\sin 20^\circ - \sqrt{3}\cos 20^\circ = 2 \Bigl(\sin 20^\circ \cdot \tfrac12 - \cos 20^\circ \cdot \tfrac{\sqrt{3}}{2}\Bigr) = 2\,\sin(20^\circ - 60^\circ) = 2\,\sin(-40^\circ).

Fakat \sin(-40^\circ) = -\sin 40^\circ olduğu için:

\sin 20^\circ - \sqrt{3}\cos 20^\circ = 2 \cdot [-\sin 40^\circ] = -2\,\sin 40^\circ.

Adım 4: Final sadeleştirme

Artık pay kısmı -2 \sin 40^\circ oldu. Payda ise \sqrt{3}\,\cos 20^\circ\,\sin 20^\circ. Ayrıca \sin 20^\circ \cos 20^\circ = \tfrac{1}{2}\,\sin(40^\circ) özdeşliğini hatırlayalım:

\sqrt{3}\,\cos 20^\circ\,\sin 20^\circ = \sqrt{3}\,\left(\frac{1}{2}\sin 40^\circ\right) = \frac{\sqrt{3}}{2}\,\sin 40^\circ.

Dolayısıyla ifade:

\frac{-2\,\sin 40^\circ}{\tfrac{\sqrt{3}}{2}\,\sin 40^\circ} = -2 \;\Big/\; \frac{\sqrt{3}}{2} = -2 \cdot \frac{2}{\sqrt{3}} = -\frac{4}{\sqrt{3}} = -\frac{4\sqrt{3}}{3}.

Yani sonuç (-4\sqrt{3}/3) olup doğru cevap (A) şıkkıdır.

Özet Tablosu

Adım İşlem/Özdeşlik Sonuç
1. Değerleri yazma cot 60° = 1/√3, ifadeyi satırlara ayırma (1/(√3 cos 20°)) - 1/sin 20°
2. Ortak payda bulma Ortak payda = √3 cos 20° sin 20° Pay: sin 20° - √3 cos 20°
3. Payı trig. özdeşlikle sadeleştirme sin 20° - √3 cos 20° = -2 sin 40°
4. Paydayı sadeleştirme cos 20° sin 20° = (1/2) sin 40°, ek olarak √3 faktörü Payda: ( √3/2 ) sin 40°
5. Nihai değer -2 sin 40° / [ ( √3/2 ) sin 40° ] = -4/√3 -4√3/3

Sonuç olarak ifade
-4√3 / 3
değerine eşittir.

@Havva_Diken