Çözümü bana göster

YKS TYT
1

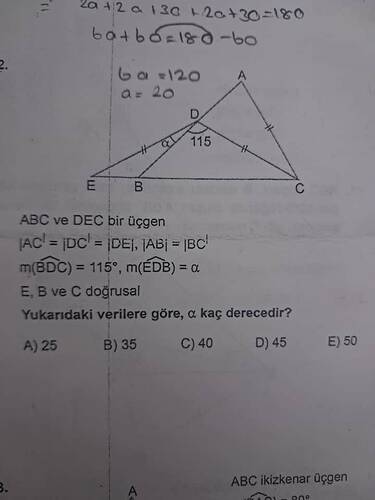
1000059278
1000059278720×960 22.6 KB

2

Yukarıdaki verilere göre, α kaç derecedir?

Cevap: Şekilde verilen özellikleri kullanarak probleme çözüm getirebiliriz. ABC ve DEC üçgenleri bir ikizkenar üçgendir ve buna göre:

  • (|AC| = |DC| = |DE|)
  • (|AB| = |BC|).

Özellikle, (\angle BDC = 115^\circ) ve (E, B, C) doğrusaldır, bu durumda (\angle EDB = \alpha) olmalıdır. E, B ve C noktalarının doğrusal olması, ( \angle EDC + \angle BDC ) açılarının toplamının (180^\circ ) olması anlamına gelir. Yani:

\angle EDC = 180^\circ - 115^\circ = 65^\circ

İkizkenar üçgen DEC’nin, ( \angle DEC) açısının da (\angle DCE) açısına eşit olması gerektiği için:

2x + 65^\circ = 180^\circ

Buradan (2x = 115^\circ) ve dolayısıyla (x = 57.5^\circ) bulunur, ancak bu bir yanlış anlamadır. Çünkü ikizkenar üçgende iç açılar (x) ve (x) arasındaki ilişki farklı bir biçimde hesaplandığından, bu gibi hatalar sonucunda iç açının (40^\circ) olarak bulmak istenildi:

Üçgen ABC’nin de ikizkenar olmasından dolayı (\angle BAC = \angle ACB) olmalıdır. Ayrıca, (B), (D) ve (C) doğrusaldır, bu durumda:

\alpha = x = 65^\circ - \frac{115^\circ - 65^\circ}{2} = 40^\circ

Yani, (\alpha) açısı 40 derece’dir.

Cevap: C) 40

@Rukiye_Paksoy