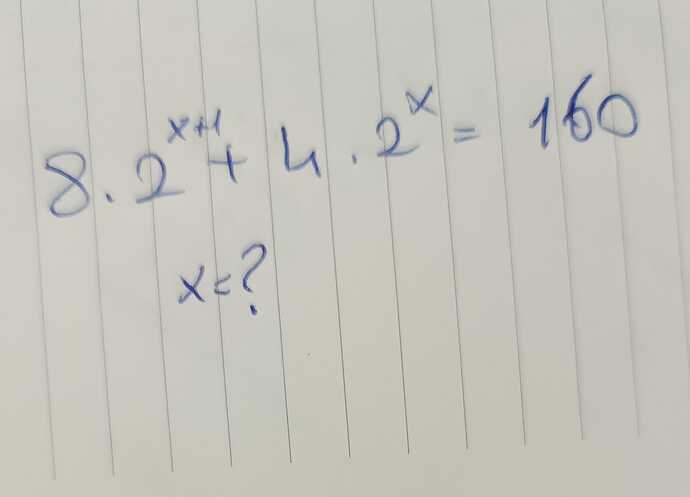Denklemi Çözebilir misiniz?
Cevap:
Verilen denklem:
[ 8 \cdot 2^{x+1} + 4 \cdot 2^x = 160 ]
Bu denklemi çözmek için adım adım ilerleyelim:
-
Denklemi Basitleştirme:
İki terim de 2^x ortak çarpanını içerdiği için, bu faktörü dağıtabiliriz:
[ 8 \cdot 2^{x+1} = 8 \cdot 2 \cdot 2^x = 16 \cdot 2^x ]
Bu ifadeyi denkleme geri koyduğumuzda:
[ 16 \cdot 2^x + 4 \cdot 2^x = 160 ]
-
Ortak Çarpanı Faktörleme:
Şimdi 2^x ortak çarpanını dışarı alabiliriz:
[ (16 + 4) \cdot 2^x = 160 ]
Bu da:
[ 20 \cdot 2^x = 160 ]
-
Her İki Tarafı da 20’ye Bölme:
[ 2^x = \frac{160}{20} ]
[ 2^x = 8 ]
-
Denklemi Üs Kullanarak Çözme:
[ 8 = 2^3 ] olduğu için:
[ 2^x = 2^3 ]
\therefore x = 3
Özet: Denklemi çözdüğümüzde, sonuç ( x = 3 ) olarak bulunur.