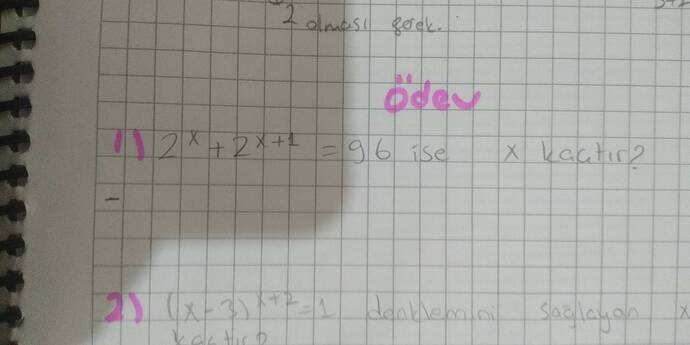Matematikmis

YKS TYT
,
1

17275188378456067736381796727745
172751883784560677363817967277454160×2080 551 KB

2

2^x + 2^(x+1) = 96 ise x kaçtır?

Çözüm Adımları:

  1. Denklemi Basitleştirin:

    • 2^{x+1} ifadesini 2^x \cdot 2^1 = 2 \cdot 2^x olarak yazabiliriz.
    • Bu durumda denklem:
      2^x + 2 \cdot 2^x = 96

  2. Ortak Çarpan Parantezine Alın:

    • 2^x ortak çarpandır, paranteze alalım:
      2^x (1 + 2) = 96
    • Bu da:
      2^x \cdot 3 = 96

  3. 2^x İçin Çözüm:

    • Her iki tarafı 3’e bölelim:
      2^x = \frac{96}{3} = 32

  4. 2^x = 32 Eşitliğinden x’i Bulun:

    • 32 sayısı 2^5'e eşittir. Böylece:
      2^x = 2^5
    • Bu durumda x = 5 olur.

x değeri \boxed{5}'tir.