Çöz iste

YKS TYT
1

17408348847246842375981092199207
17408348847246842375981092199207720×960 30.8 KB

2

Sorunun Çözümü:

Soruda verilen bilgilere göre, ödevimiz A saksısının tabanının zeminden yüksekliğini bulmaktır. Problemde paylaşılan bilgiler ve şekle göre saksi yüksekliği katman katman sorunun çözümüne katkı sağlar.

1. Verilen Bilgiler:

  1. Her bir saksının yüksekliği: \frac{1}{5} metre
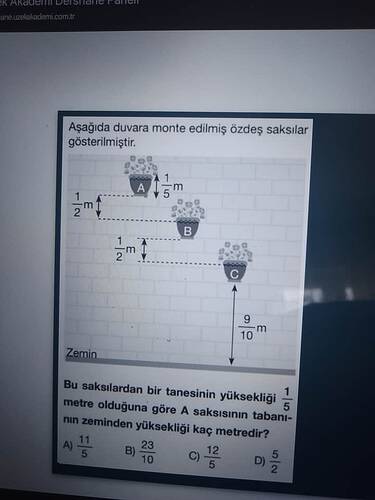
  2. Saksıların zeminle olan mesafeleri şekil üzerinden belirlenmiş:
    • C saksısı: Yerden \frac{9}{10} m yükseklikte.
    • C saksısının üst kenarından, B saksısının tabanına olan mesafe: \frac{1}{2} m.
    • B saksısından, A saksısının tabanına olan mesafe: 1 \, \text{metre}.

2. Çözüm Aşaması:

Adım 1: C Saksısının Tepesinin Yüksekliği

C saksısının zeminden yükseklik bilgisi verilmiş:

C \, (taban): \frac{9}{10} \, \text{metre}.

C saksısının tepe yüksekliğini bulabilmek için, saksının kendi yüksekliği olan \frac{1}{5} metreyi eklersiniz. Bu durumda C saksısının üst yüksekliği şu şekilde bulunur:

C \, (üst): \frac{9}{10} + \frac{1}{5}.

Payda eşitleyelim:

\frac{9}{10} + \frac{1}{5} = \frac{9}{10} + \frac{2}{10} = \frac{11}{10}.

Sonuç: C saksısının üst kenarı zeminden \frac{11}{10} \, \text{metre} yükseklikte.

Adım 2: B Saksısının Taban Yüksekliği

C saksısının üst kenarından B saksısının tabanına olan yükseklik verilmiştir: \frac{1}{2} \, \text{metre} .

Bu yükseklik C saksısının üst yüksekliğine eklenerek, B saksısının taban yüksekliği bulunur:

B \, (taban) = C \, (üst) + \frac{1}{2}.

Buradan:

B \, (taban) = \frac{11}{10} + \frac{1}{2}.

Payda eşitleyelim:

\frac{11}{10} + \frac{1}{2} = \frac{11}{10} + \frac{5}{10} = \frac{16}{10}.

Sadedeştirirsek:

B \, (taban) = \frac{8}{5} \, \text{metre}.

Adım 3: A Saksısının Taban Yüksekliği

Şimdi B saksısından A saksısının tabanına olan mesafe verilmiş: 1 \, \text{metre}.

Bu mesafe, B saksısının taban yüksekliğine eklenir:

A \, (taban) = B \, (taban) + 1.

Buradan:

A \, (taban) = \frac{8}{5} + 1.

Payda eşitleyelim:

\frac{8}{5} + 1 = \frac{8}{5} + \frac{5}{5} = \frac{13}{5}.

4. Sonuç:

A saksısının tabanının zeminden yüksekliği \frac{13}{5} metredir.

Doğru Cevap: A) \frac{11}{5}