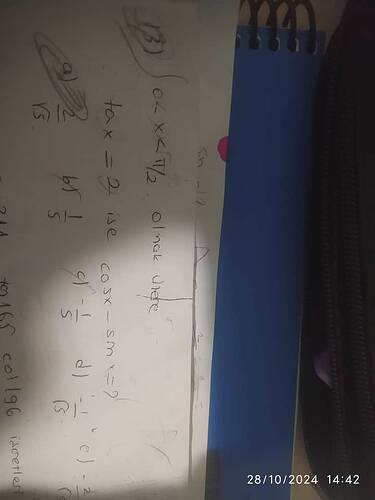Görselde trigonometri ile ilgili bir problem var. Görüldüğü üzere, \tan(x) = 2 ifadesi verilmiş ve 0 \leq x \leq \frac{\pi}{2} aralığında cos(x) - \sin(x) ifadesinin değeri soruluyor.
İşlemi çözmek için şu adımları izleyelim:
-
Tanımları Kullanarak Başlayalım:
\tan(x) = \frac{\sin(x)}{\cos(x)} = 2 olarak verilmiş.
Buradan \sin(x) = 2\cos(x) elde edebiliriz.
-
Trigonometrik Kimlik ve İfadeyi Basitleştirme:
\sin^2(x) + \cos^2(x) = 1 kimliğini kullanarak, yerine koyma yaparak çözebiliriz.
\sin(x) = 2\cos(x) olduğuna göre, bu ifadeyi sinüs yerine koyabiliriz:
$$(2\cos(x))^2 + \cos^2(x) = 1$$
$$4\cos^2(x) + \cos^2(x) = 1$$
$$5\cos^2(x) = 1$$
Buradan \cos^2(x) = \frac{1}{5} ve dolayısıyla \cos(x) = \frac{1}{\sqrt{5}} (pozitif çünkü 0 \leq x \leq \frac{\pi}{2}).
-
Sinüs Değerini Bulma:
\sin(x) = 2\cos(x) = 2 \times \frac{1}{\sqrt{5}} = \frac{2}{\sqrt{5}}
-
İstenen İfadeyi Hesaplama:
cos(x) - \sin(x) = \frac{1}{\sqrt{5}} - \frac{2}{\sqrt{5}} = -\frac{1}{\sqrt{5}}
Bu da \frac{-\sqrt{5}}{5} olarak sadeleştirilir.
Sonuç:
Bu işlemlere göre, cos(x) - \sin(x) ifadesinin değeri -\frac{\sqrt{5}}{5}'tir.