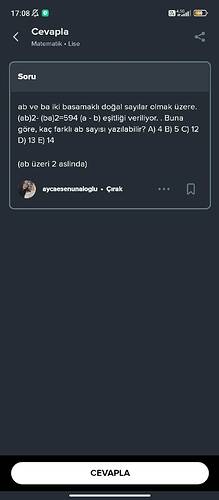
Bu soruda, iki basamaklı ab ve ba sayılarının karesi arasındaki fark ile rakamlar arasındaki farkın çarpımı verilmiş. Bunu çözelim.
Çözüm:
abiki basamaklı sayısını 10a + b olarak yazabiliriz.baise 10b + a olur.
Verilen denklem:
(10a + b)^2 - (10b + a)^2 = 594(a - b)
- Kaç farklı
absayısı yazılabileceğini bulmalıyız. Bunun için önce denklem üzerinde düzenlemeler yapalım:
(10a + b)^2 = 100a^2 + 20ab + b^2
(10b + a)^2 = 100b^2 + 20ba + a^2
Farkı alırsak:
100a^2 + 20ab + b^2 - (100b^2 + 20ba + a^2) = 594(a - b)
99a^2 + 20ab + b^2 - 100b^2 - 20ab - a^2 = 594(a - b)
99a^2 - 99b^2 = 594(a - b)
- Faktoring yapalım:
99(a^2 - b^2) = 594(a - b)
- a^2 - b^2 = (a - b)(a + b) faktörizasyonunu kullanarak:
99(a - b)(a + b) = 594(a - b)
a - b sıfır olmadığı sürece sadeleştirilebilir:
99(a + b) = 594
- Her iki tarafı 99’a bölelim:
a + b = 6
Sonuç
a + b = 6 olacak şekilde çiftler:
- (1, 5)
- (2, 4)
- (3, 3)
- (4, 2)
- (5, 1)
Bu durumda ab sayısı olabilecek değerler:
- 15
- 24
- 33
- 42
- 51
Bu kombinasyonlara göre 5 farklı ab sayısı yazılabilir.
Final Cevap:
5 farklı ab sayısı yazılabilir. (B seçeneği)