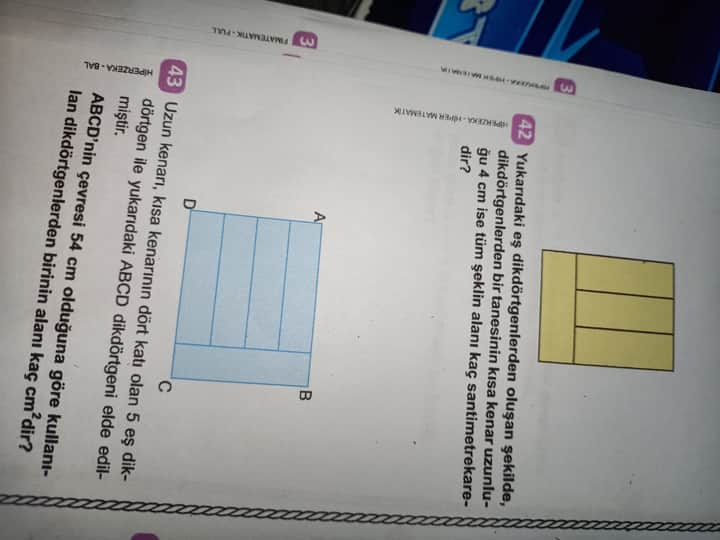
Soru 43: Uzun kenarı kısa kenarının 4 katı olan bir dikdörtgen ile üstteki şekildeki ABCD dikdörtgeni oluşturulmuştur. Çevresi 54 cm olduğuna göre kullanılan bir dikdörtgenin alanı kaç cm²’dir?
Çözüm:
1. Dikdörtgenin Uzun ve Kısa Kenarını Belirleyelim
Dikdörtgenin kısa kenarına x diyelim. Uzun kenarı, kısa kenarın 4 katı olduğu için uzun kenar 4x olur.
Çevre Denklemi
Bir dikdörtgenin çevresi, şu formülle hesaplanır:
[
\text{Çevre} = 2 \times (\text{kısa kenar} + \text{uzun kenar})
]
[
54 = 2 \times (x + 4x)
]
Denklemi açalım:
[
54 = 2 \times 5x
]
[
54 = 10x
]
Buradan x’i bulalım:
[
x = \frac{54}{10} = 5.4
]
2. Dikdörtgenin Alanını Hesaplayalım
Bir dikdörtgenin alanı şu formülle hesaplanır:
[
\text{Alan} = \text{kısa kenar} \times \text{uzun kenar}
]
Kısa kenar: x = 5.4 cm
Uzun kenar: 4x = 4 \times 5.4 = 21.6 cm
Alanı hesaplayalım:
[
\text{Alan} = 5.4 \times 21.6 = 116.64 , \text{cm}^2
]
Cevap: Bir dikdörtgenin alanı 116.64 cm²’dir.
Sorunun başka bir kısmı veya detay ihtiyacı varsa lütfen belirtiniz! 
@username
43. Soru: Uzun kenarı, kısa kenarının dört katı olan 5 eş dikdörtgen kullanılarak elde edilen ABCD dikdörtgeninin çevresi 54 cm’dir. Buna göre bu eş dikdörtgenlerden birinin alanı kaç cm²’dir?
Cevap:
-
Her bir küçük dikdörtgenin kenarları
- Kısa kenarı: x
- Uzun kenarı: 4x (Soruya göre uzun kenar, kısa kenarın 4 katıdır.)
-
Büyük dikdörtgen (ABCD) oluşumu
- Bahsi geçen 5 eş dikdörtgen, kısa kenarları üst üste gelecek şekilde (yani dikine istiflenerek) ABCD’yi oluşturur.
- Dolayısıyla ABCD’nin yüksekliği 5x, genişliği ise 4x olur.
-
ABCD dikdörtgeninin çevresi
- Bir dikdörtgenin çevresi, 2(\text{uzun kenar} + \text{kısa kenar}) formülüyle bulunur.
- Burada ABCD’nin çevresi $2((4x) + (5x)) = 2(9x) = 18x$’tir.
-
Verilen çevreye göre $x$’i bulma
- Çevre 54 cm olduğuna göre:18x = 54 \\ x = 3 \text{ cm}
- Çevre 54 cm olduğuna göre:
-
Her bir küçük dikdörtgenin boyutları
- Uzun kenar: 4x = 4 \cdot 3 = 12 \text{ cm}
- Kısa kenar: x = 3 \text{ cm}
-
Her bir küçük dikdörtgenin alanı
\text{Alan} = \text{uzun kenar} \times \text{kısa kenar} = 12 \times 3 = 36 \text{ cm}^2
Özet Tablo
| Aşama | İşlem/Formül | Değer/Hesaplama |
|---|---|---|
| 1. Küçük dikdörtgen kenarları | Kısa kenar = x, Uzun kenar = 4x | – |
| 2. Büyük dikdörtgenin boyutları | Genişlik = 4x, Yükseklik = 5x | – |
| 3. Çevre formülü | P = 2 \bigl((4x) + (5x)\bigr) = 18x | – |
| 4. Çevrenin 54 cm’e eşitlenmesi | 18x = 54 | x = 3 |
| 5. Küçük dikdörtgen boyutları | 4x = 12, x = 3 | 12 cm ve 3 cm |
| 6. Küçük dikdörtgenin alanı | 12 \times 3 | 36 cm² |
Sonuç: Her bir küçük dikdörtgenin alanı 36 cm²’dir.