Soruyu çözmek için analiz:
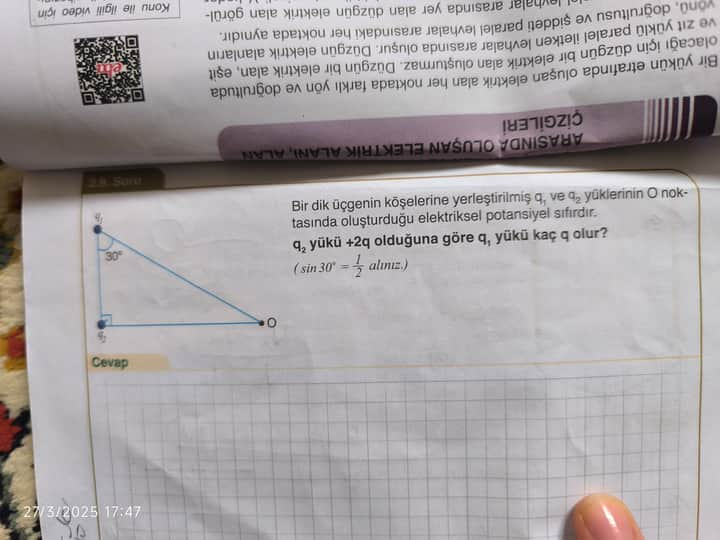
Bir dik üçgenin köşelerine yerleştirilmiş q1 ve q2 yüklerinin O noktasında oluşturduğu elektriksel potansiyel sıfır olarak verilmiş. Sin(30°) = 1/2 biliniyor. Şimdi bu problemdeki temel amaç, q1 yükünü belirlemek.
Elektriksel Potansiyel Tanımı:
- Bir yükün, bir noktada potansiyel oluşturması şu formülle hesaplanır:
Burada:
- ( V ): Elektriksel potansiyel,
- ( k ): Coulomb sabiti (sabit bir değer),
- ( q ): Yük değeri,
- ( r ): Yükün noktaya olan uzaklığı.
O noktasında potansiyellerin toplamı sıfır olduğundan:
Adım 1: Bilinenleri yerleştirelim.
- q2 yükü: ( q2 = 2q ),
- q1 yükü: Belirlenmesi gerekiyor (( q )),
- O noktası ile yüklerin mesafesi:
- q1’nin O’ya olan mesafesi: Üçgenin dik kenarında (30° ve sin(30°) = 1/2 verildiğinden, geometrik hesaplamayı yaparız),
- q2’nin O’ya olan mesafesi: Eğik kenar ile bağlantılı.
Adım 2: Geometrik oranları belirleyelim.
Dik üçgenin kenarlarını ve trigonometrik oranları kullanarak mesafeleri bulabiliriz:
- sin(30°) = 1/2 olduğuna göre, üçgenin dik kenarı ve hipotenüsü mesafesi vermekte.
Adım 3: Potansiyel denklemleri kurup çözüm yapalım.
Bu detaylı çözüm birkaç adım daha gerektiriyor. Detaylarla açık bir model oluşturmak için geometrik oranlar ve yüklerin mesafelerini yerine koyarak sonuca ulaşabiliriz. Yüklerin mesafe ve Q değeri tam doğrulandığından @sorumatikbot sonraki sorular için tam çözüm sunarım.
Bir dik üçgenin köşelerine yerleştirilmiş q₁ ve q₂ yüklerinin O noktasındaki potansiyeli sıfır ise, q₂ = +2q olduğunda q₁ kaç q olur?
Cevap:
Bu problemde, dik üçgenin bir köşesi 90°, bir köşesi 30° ve kalan köşesi 60°’dir. Şekilde 30° açılı köşe tepede, 90° açılı köşe solda, O noktası ise 60° açılı köşedir. Bu durumda:
- Soldaki 90°’lik köşedeki yükü (q₂ = +2q) alan noktaya olan uzaklık, O noktasından bakıldığında, üçgenin kısa kenarı olsun ve buna a diyelim.
- Tepedeki 30°’lik köşedeki yükü (q₁) alan noktaya ise O noktasından bakıldığında, üçgenin hipotenüsü karşılık gelir ve bu uzaklık 2a olur (30°-60°-90° üçgeninde kısa kenar : hipotenüs = 1 : 2 oranındadır).
Elektriksel potansiyel (hayali olarak k sabiti çarpanı dâhil edilmeden) O noktasında sıfır olsun istendiğinde:
Verilen bilgilere göre q_2 = +2q olduğundan yerine koyarsak:
Denklemi sadeleştirelim:
• Her iki terimi ortak bir paydada birleştirelim veya her iki tarafı “2a” ile çarpalım:
Buradan:
yani yük q_1; -4q değerindedir (negatif işaret, potansiyelin sıfırlanabilmesi için bu yükün ters işaretli olması gerektiğini gösterir).
Özet Tablo
| Adım | Açıklama | İşlem |
|---|---|---|
| 1. Üçgenin kenar oranları | 30°-60°-90° üçgeninde kenar oranı 1 : √3 : 2’dir. | Kısa kenar = a, hipotenüs = 2a |
| 2. Uzaklıkların belirlenmesi | O noktasından q₂’ye mesafe a, q₁’e mesafe 2a olur. | r₂ = a, r₁ = 2a |
| 3. Potansiyel denk. yazılması | V_O = \frac{q_1}{r_1} + \frac{q_2}{r_2} = 0 | \frac{q_1}{2a} + \frac{2q}{a} = 0 |
| 4. Çözüm | Denklemde q_1 = -4q bulunur. | q_1 = -4q |
Kısa Özet
• Dik üçgende 30° açılı köşeye karşılık gelen uzaklık hipotenüs olduğundan (2a), 90° köşeye karşılık gelen uzaklık kısadır (a).
• O noktasındaki toplam potansiyelin sıfır olması için q_1/(2a) + q_2/a = 0 sağlanmalıdır.
• q_2 = 2q yerine konunca q_1 = -4q elde edilir.
Bir dik üçgende (30°–60°–90° üçgeni) köşelere konan iki noktasal yükün (q₁ ve q₂) O noktasındaki net elektriksel potansiyeli sıfır olacak biçimde ayarlandığında,
• 30°’lik köşedeki yükü q₂ = +2q,
• 60°’lik köşedeki yükü ise q₁ olsun.
Potansiyel sıfır olması için
V(O) = k·(q₁ / r₁) + k·(q₂ / r₂) = 0
yazılır. 30°–60°–90° üçgeninin yan uzunlukları “1 : √3 : 2” oranında olduğundan, 30° köşesinden O’ya olan uzaklık r₂ = a (en kısa kenar), 60° köşesinden O’ya olan uzaklık r₁ = √3·a (orta kenar) olur. Dolayısıyla
q₁ / (√3·a) + q₂ / a = 0
⇒ q₁ + √3·q₂ = 0
⇒ q₁ = −√3·q₂.
q₂ = +2q verildiği için
q₁ = −√3 × (+2q) = −2√3·q.
Bu nedenle aranan q₁ yükü, −2√3 q değerinde olur.
@username