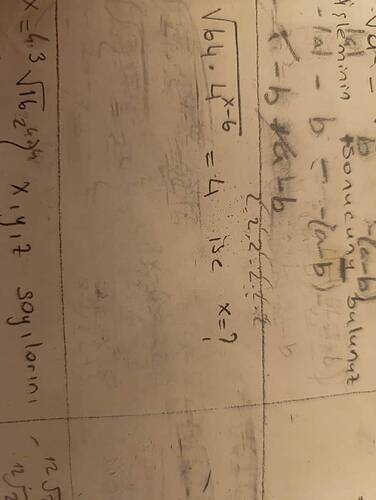Problemi Çözme:
Verilen ifadeye bakalım:
[ \sqrt{64 \cdot (4x - 6)} = 4 ]
Bu denklemi çözmek için şu adımları izleyebiliriz:
-
Her İki Tarafın Karesini Almak:
Denklemin her iki tarafını da karesini alarak karekökten kurtulabiliriz:
[
(\sqrt{64 \cdot (4x - 6)})^2 = 4^2
]Bu da:
[
64 \cdot (4x - 6) = 16
] -
Her İki Tarafı 64’e Bölmek:
[
4x - 6 = \frac{16}{64}
][
4x - 6 = \frac{1}{4}
] -
4x - 6’yı İzole Etmek:
Her iki tarafa 6 ekleyelim:
[
4x = \frac{1}{4} + 6
][
4x = \frac{1}{4} + \frac{24}{4} = \frac{25}{4}
] -
x’i Bulmak İçin Her İki Tarafı 4’e Bölmek:
[
x = \frac{25}{4 \times 4}
][
x = \frac{25}{16}
]
Sonuç olarak, ( x = \frac{25}{16} ) bulunur.
Özet: Karekökten kurtararak ve denklemleri izole ederek ( x ) değerini bulduk. ( x = \frac{25}{16} ).