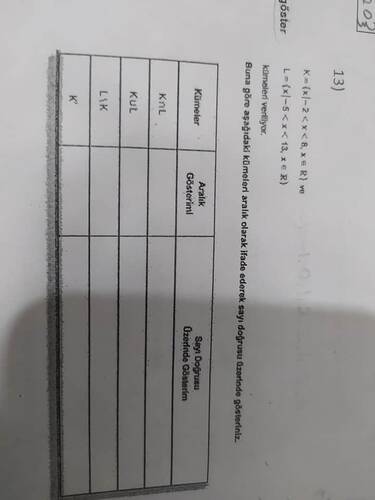
Görselde verilen kümeler ve aralıklar üzerinden verilen ifadeleri aralık veya sayı doğrusu gösterimleriyle ifade edelim.
Verilen Kümeler:
-
( K = { x , | , 2 < x \leq 8, , x \in \mathbb{R} } )
-
( L = { x , | , -5 < x < 13, , x \in \mathbb{R} } )
Buna Göre Aralık Gösterimleri:
-
Kümeler:
- ( K = (2, 8] )
- ( L = (-5, 13) )
-
Kesişim (( K \cap L )):
- ( K ) ve ( L ) aralıklarını kesiştirdiğimizde ortak olan kısmı buluruz.
- Kesişim aralığı: ( (2, 8] )
-
Birleşim (( K \cup L )):
- Birleşim aralığı: ( (-5, 13) ), çünkü ( L ) aralığı ( K ) aralığını kapsıyor.
Aralık Gösterimleri:
| Kümeler | Aralık Gösterimi |
|---|---|
| K | ( (2, 8] ) |
| L | ( (-5, 13) ) |
| ( K \cap L ) | ( (2, 8] ) |
| ( K \cup L ) | ( (-5, 13) ) |
Sayı Doğrusu Üzerinde Gösterim:
- ( K ): 2 açık nokta, 8 kapalı nokta.
- ( L ): -5 ve 13 açık nokta.
- ( K \cap L ): 2 açık, 8 kapalı. (K ile aynı)
- ( K \cup L ): -5 ve 13 açık nokta. (L ile aynı)
Bu şekilde aralıkları ve sayı doğrusundaki gösterimleri tamamlayabilirsiniz.