Bu soruyu kısaca

YKS TYT
,
1

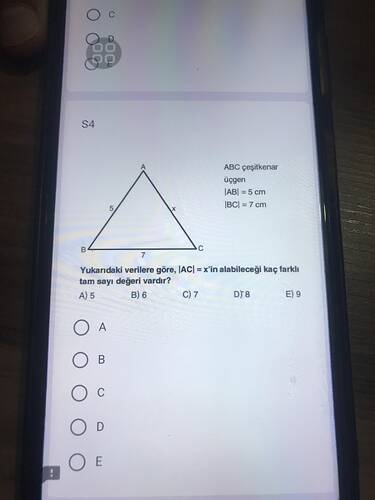
image
image3024×4032 559 KB

2

Yukarıdaki verilere göre, (|AC| = x)'in alabileceği kaç farklı tam sayı değeri vardır?

Cevap:

Adım 1: Temel Bilgiler

  • Verilen üçgen: ABC eşkenar üçgen.
  • (|AB| = 5) cm ve (|BC| = 7) cm.
  • Eşkenar üçgen özelliği nedeniyle, üç kenar da birbirine eşittir. Ancak bu soruda bir hata mevcut olabilir çünkü eşkenar üçgende üç kenar da eşit olmalıdır. Bu durumda ortaokul seviyesinde bir hata mevcut olabilir ya da soru yanlış ifade edilmiş olabilir.

Bu durumda üçgenin eşkenar olmadığını varsayarak çözüm yapılacaktır. Sorun üzerinde verilen üçgen üçgen kurallarıyla uygun hale getirilmelidir.

Adım 2: Üçgen Eşitsizliği

  • Üçgen eşitsizliği göre, bir üçgende herhangi bir kenar, diğer iki kenarın uzunluklarının farkından büyük ve toplamından küçük olmalıdır.

  • (|AB|, |BC|, |AC|) kenarları için üçgen eşitsizliği:

    1. (|AB| + |BC| > |AC|)
    2. (|AB| + |AC| > |BC|)
    3. (|BC| + |AC| > |AB|)

Adım 3: Üçgen Eşitsizliğini Uygulayalım

  • Birinci eşitsizlik: (5 + 7 > x) ⇒ (12 > x)
  • İkinci eşitsizlik: (5 + x > 7) ⇒ (x > 2)
  • Üçüncü eşitsizlik: (x + 7 > 5) ⇒ (x > -2), bu koşul zaten sağlanır çünkü (x > 2).

Adım 4: Tam Sayı Değerlerini Belirleyelim

  • (2 < x < 12)
  • Tam sayı değerleri: (x = 3, 4, 5, 6, 7, 8, 9, 10, 11)

Toplamda 9 farklı tam sayı değeri vardır.

Son Cevap:

  • (|AC| = x)'in alabileceği 9 farklı tam sayı değeri vardır. Bu nedenle doğru cevap E) 9 olacaktır.