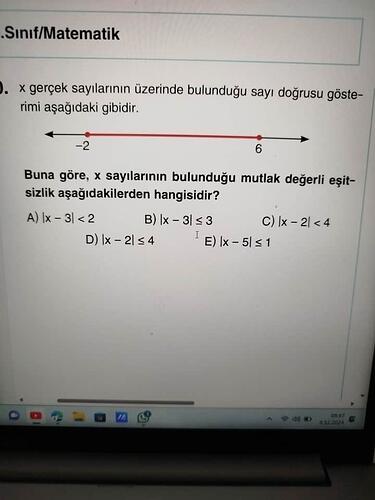
x gerçek sayılarının üzerinde bulunduğu sayı doğrusu gösterimi yukarıda verilmiştir. Verilen bilgiye göre x sayılarının bulunduğu mutlak değerli eşitsizlik aşağıdakilerden hangisidir?
Görüntüden anladığımız kadarıyla, x sayıları -2 ile 6 arasında yer alıyor. Bu bilgiye göre aşağıdaki adımları izleyerek doğru eşitsizliği belirleyebiliriz:
-
Eşitsizliği Merkezi Konumda Düşünme:
Sayı doğrusu üzerinde -2 ile 6 arasında bir aralık verilmiş. Bu aralığın merkezi, x değerleri için en uygun temsil edilen nokta olabilir. İki uç noktanın (6 ve -2) ortasını bularak merkezi belirleriz:
\text{Orta Nokta} = \frac{-2 + 6}{2} = 2 -
Aralık Yarıçapı Hesaplama:
Merkezi bulduktan sonra, bu noktanın sağa veya sola olan uzaklığı eşitsizliğin “yarıçapını” belirleyecektir. Yani merkezden en uzak uç noktayı buluruz:
\text{Yarıçap} = 6 - 2 = 4 \quad \text{(veya aynı şekilde $2 - (-2) = 4$)} -
Doğru Eşitsizliğin Seçimi:
Bulduğumuz merkez ve yarıçap ile eşitsizlik formunu yazabiliriz:
|x - \text{Merkez}| \leq \text{Yarıçap}Bu formül, genel olarak |x - 2| \leq 4 şeklinde olacaktır. Bu nedenle doğru seçenek D şıkkıdır.
Sonuç olarak, doğru cevap: D) |x - 2| \leq 4.