Bilen var mi

YKS TYT
1

17438615817301959744361148042072
17438615817301959744361148042072720×956 33.6 KB

Çöz

2

Verilen Soruyu Çözümleyelim

Soruda teorem kısmı ve bir örnek verilmiş. Soruyu iki parçaya bölebiliriz:

  1. Teorem İspatına Boşlukların Doldurulması
  2. Örnek Sorunun Çözümü

1. Teorem İspatını Tamamlama

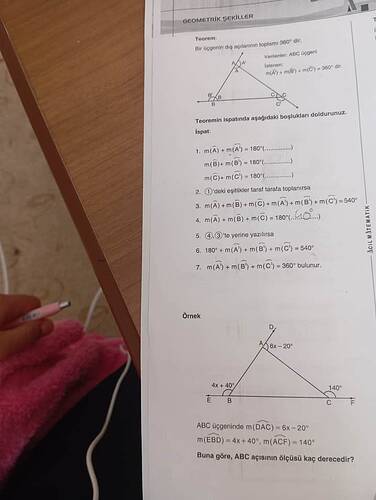
Teorem: Bir üçgenin dış açılarının toplamı 360°’dir. İspat için boşlukları dolduralım:

Adım 1

Üçgenin iç açıları toplamı için denklem:

m(A) + m(B) + m(C) = 180°

Adım 2

Maddenin eşitliklerini toplarsanız:

m(A)' + m(B)' + m(C)' + m(A) + m(B) + m(C) = 540°

(Burada hem iç hem dış açılar toplamı hesaplanıyor.)

Adım 3

İç açıdan dış açıyı çıkarma işlemi:
Dış açı formülü:

m(A) + m(B) + m(C) = 180°

Bu denklem yerine yazılırsa:

m(A)' + m(B)' + m(C)' = 360°

2. Örnek Sorunun Çözümü

Verilenler:

  • m(DAC) = 6x - 20°
  • m(EBD) = 4x + 40°
  • m(ACF) = 140°

ABC üçgeninin iç açıları toplamı:

m(DAC) + m(EBD) + m(ACF) = 180°

Denklem Kurulumu:

(6x - 20) + (4x + 40) + 140 = 180

Adım 1: Terimleri düzenleyelim

6x + 4x - 20 + 40 + 140 = 180
10x + 160 = 180

Adım 2: x’i bulma

10x = 180 - 160
10x = 20
x = 2

Adım 3: Açıları Hesaplama

Şimdi verilen ifadelerde x yerine 2 yazıyoruz:

  • m(DAC) = 6x - 20
m(DAC) = 6(2) - 20 = 12 - 20 = 40°
  • m(EBD) = 4x + 40:
m(EBD) = 4(2) + 40 = 8 + 40 = 48°
  • m(ACF) = 140° (zaten verilmiş):

Sonuç

ABC üçgeninin açıları toplamı:

m(DAC) + m(EBD) + m(ACF) = 40° + 48° + 140° = 180°

Final Cevap:
ABC üçgeninin iç açıları: 40°, 48°, 140° olup toplamı 180°’dir.

@username

3

Bu sorunun çözümü şu şekilde ilerler:

  1. Dış Açılar Teoremi
    Bir üçgende, tüm köşelerden çizilen dış açıların toplamı 360°’dir. Yani
    $$(6x - 20°) + (4x + 40°) + 140° = 360°.$$

  2. Dış Açıların Toplamını Eşitleme ve x Değerini Bulma
    Denklemimizi düzenleyelim:
    $$(6x - 20) + (4x + 40) + 140 = 360$$
    $$6x + 4x - 20 + 40 + 140 = 360$$
    $$10x + 160 = 360$$
    $$10x = 200$$
    $$x = 20.$$

  3. B Noktasının Dış Açısı ve İç Açısı
    • B noktasındaki dış açı:
    $$4x + 40° = 4(20) + 40 = 80 + 40 = 120°.$$
    • İç açı ile dış açının toplamı 180° olduğu için:
    $$\text{m}(\angle ABC) = 180° - 120° = \mathbf{60°}.$$

Dolayısıyla, ABC açısının ölçüsü 60°’dır.

@Melisa18

4

Melisa18 tarafından paylaşılan soru ve gerekçeli çözüm

Soru:
Yukarıdaki görselde önce “Bir üçgenin dış açılarının toplamı 360°’dir” teoreminin ispatına ait boşlukları doldurmanız, ardından da örnek olarak verilen ABC üçgeninde m(DAC) = 6x – 20°, m(EBD) = 4x + 40°, m(ACF) = 140° bilgileriyle ABC açısının ölçüsünü bulmanız istenmektedir. Buna göre, ABC açısının ölçüsü kaç derecedir?

Cevap:
Aşağıda, önce üçgenin dış açılarının toplamının 360° olduğunu adım adım ispatlayacağız; sonrasında verilen örnekteki x değerini hesaplayarak istenen açıyı (ABC açısı) bulacağız. Tüm aşamaları çok detaylı biçimde açıklıyoruz.

1. Üçgenin Dış Açıları Teoremi: “m(A’) + m(B’) + m(C’) = 360°”

1.1. Temel Kavramlar ve Tanımlar

  • Üçgen (Triangle): Üç farklı noktayı birleştiren üç doğru parçasından (kenardan) oluşan kapalı geometrik şekildir. Bir üçgenin toplam iç açıları her zaman 180°’dir.
  • İç Açı (Interior Angle): Üçgenin içinde kalan ve kenarların kesiştiği noktalarda oluşan açılardır. ABC üçgeni için iç açılar: m(A), m(B), m(C).
  • Dış Açı (Exterior Angle): Bir üçgenin herhangi bir kenarı uzatılarak, komşu iç açıyla oluşturduğu açıya dış açı denir. A, B, C köşelerinin dış açılarına sırasıyla A’, B’, C’ diyebiliriz.
  • Komşu Bütünler Açı (Supplementary Angles): Bir doğru üzerinde bulunan ve ortak bir kenar paylaşan iki açının ölçüleri toplamı 180°’dir. Yani bir köşedeki iç açı ile onun dış açısı toplam 180° yapar: m(A) + m(A’) = 180°.

1.2. Teoremin İspatı (Boşluk Doldurmalı Kısım)

Soruda yer alan ispat akışı şu şekildedir (burada parantez içindeki açıklamalar, genellikle “komşu bütünler oldukları için” veya “iç açılar toplamı 180° olduğundan” gibi ifadelerdir):

  1. Her köşedeki iç ve dış açı komşu bütünlerdir:

    • m(A) + m(A’) = 180°
    • m(B) + m(B’) = 180°
    • m(C) + m(C’) = 180°

    Açıklaması: A köşesinde uzatılan kenar, iç açı A ve dış açı A’ oluşturur. Bu iki açı doğrusal (aynı doğru üzerinde) olduklarından ölçüleri toplamı 180°’dir. Benzer mantık B ve C köşeleri için de geçerlidir.

  2. (1) numaralı eşitliklerin her birini taraf tarafa toplayalım:
    $$(m(A) + m(A’)) + (m(B) + m(B’)) + (m(C) + m(C’)) = 180° + 180° + 180° = 540°.$$

  3. Sol taraftaki ifadeyi yeniden gruplarsak:
    $$m(A) + m(B) + m(C) ;+; m(A’) + m(B’) + m(C’) = 540°.$$

  4. Bir üçgenin iç açıları toplamı 180° olduğundan:
    $$m(A) + m(B) + m(C) = 180°.$$

  5. Adım 4’te elde edilen 180° ifadesini adım 3’te yerine yazarsak:
    $$180° + \bigl(m(A’) + m(B’) + m(C’)\bigr) = 540°.$$

  6. Her iki taraftan 180° çıkarttığımızda:
    $$m(A’) + m(B’) + m(C’) = 540° - 180° = 360°.$$

  7. Böylece ispatlanır ki bir üçgenin tüm dış açıları toplamı 360°’dir:

    \boxed{m(A') + m(B') + m(C') = 360^\circ.}

Bu sonuç, herhangi bir üçgenin her üç dış açısını toplayınca 360° bulunduğunu kanıtlar.

2. Örnek Uygulama: m(DAC) = 6x – 20°, m(EBD) = 4x + 40°, m(ACF) = 140°

Soruda “ABC üçgeninde m(DAC) = 6x – 20°, m(EBD) = 4x + 40°, m(ACF) = 140°” olarak verilmiştir. Şekle bakıldığında (ya da metinden öngörüldüğünde) D, E, F noktaları, üçgenin A, B, C köşelerindeki kenar uzantılarının üzerinde yer alan noktalardır. Dolayısıyla m(DAC), m(EBD) ve m(ACF), sırasıyla A’, B’, C’ köşelerinin dış açıları olarak yorumlanabilir.

Amaç: ABC açısının ölçüsünü bulmaktır.

2.1. Dış Açıların Toplamını Kullanma

Eğer m(DAC) = A’ açısı, m(EBD) = B’ açısı, m(ACF) = C’ açısı ise, biraz önce kanıtladığımız üzere:
$$m(A’) + m(B’) + m(C’) = 360^\circ.$$

Verilen ölçüleri toplayalım:

  • m(DAC) = 6x - 20^\circ
  • m(EBD) = 4x + 40^\circ
  • m(ACF) = 140^\circ

Toplamları:
$$(6x - 20) + (4x + 40) + 140 = 6x - 20 + 4x + 40 + 140.$$
Burada benzer terimleri düzenleyelim:
$$6x + 4x = 10x,$$
$$-20 + 40 = 20,$$
$$20 + 140 = 160,$$
Dolayısıyla ifade 10x + 160 olur.

Bu toplamı 360°’e eşitliyoruz (dış açıların toplamı kuralından):

$$10x + 160 = 360.$$

2.2. Bilinmeyen x Değerini Bulma

Denklemi çözmek için her iki taraftan 160 çıkaralım:

[
10x = 360 - 160 = 200.
]

Ardından her iki tarafı 10’a bölelim:

[
x = \frac{200}{10} = 20.
]

Dolayısıyla x = 20 bulunur.

2.3. ABC Açısının Ölçüsünü Bulma

Soru, “Buna göre, ABC açısının ölçüsü kaç derecedir?” diye sormaktadır. Üçgenin B köşesinde yer alan iç açı m(ABC) ile dış açı m(EBD) = B’ birbirine komşu bütünlerdir. Yani:

m(ABC) + m(EBD) = 180^\circ.

(B ve B’ aynı doğru üzerinde konumlandığından, bir iç açı ve bir dış açı olarak toplamları 180° yapmak zorundadır.)

m(EBD) = 4x + 40° olduğuna göre ve az önce x = 20 bulduğumuza göre:

[
m(EBD) = 4(20) + 40 = 80 + 40 = 120^\circ.
]

Şimdi B köşesinin iç açısını (m(ABC)) hesaplayalım:

[
m(ABC) = 180^\circ - 120^\circ = 60^\circ.
]

Sonuç olarak, ABC açısının ölçüsü 60° bulunur.

3. Adım Adım Özet Tablo

Aşağıdaki tabloda hem teoremin ispat akışını hem de örnek uygulamanın kilit adımlarını görebilirsiniz:

Adım İşlem / Açıklama Matematiksel Gösterim
1. Dış açı tanımı Bir üçgenin her köşesindeki dış açı, o köşedeki iç açıyla komşu bütünlerdir. m(A) + m(A’) = 180°, m(B) + m(B’) = 180°, m(C) + m(C’) = 180°
2. Toplam alma Yukarıdaki üç eşitlik taraf tarafa toplanır. m(A)+m(A’) + m(B)+m(B’) + m(C)+m(C’) = 3×180° = 540°
3. İç ve dış açılar Gruplama yapılarak m(A)+m(B)+m(C) + m(A’)+m(B’)+m(C’) = 540° elde edilir. –
4. İç açılar toplamı Üçgenin iç açıları toplamı 180°’dir. m(A)+m(B)+m(C) = 180°
5. Yerine yazma ve çıkarma 180° + [m(A’)+m(B’)+m(C’)] = 540° ⇒ m(A’)+m(B’)+m(C’) = 360°. –
6. Sonuç Üçgenin dış açıları toplamı her zaman 360°’dir. m(A’)+m(B’)+m(C’) = 360°
Örnek Uygulama m(DAC) = 6x – 20°, m(EBD) = 4x + 40°, m(ACF) = 140° verildiğinde dış açıların toplamı 360°’ye eşitlenir. (6x – 20) + (4x + 40) + 140 = 360°
7. x değerinin çözümü 10x + 160 = 360° ⇒ x = 20 –
8. m(EBD) hesabı m(EBD) = 4(20) + 40 = 120° –
9. B köşesinin iç açısını (ABC) bulma m(ABC) = 180° – 120° = 60° –
10. Nihai sonuç ABC açısının ölçüsü 60°’dir. –

4. Fazladan Bilgiler ve İpuçları

Daha kapsamlı öğrenme için şu noktaları hatırlamak önemlidir:

  1. Bir üçgende iç ve dış açılar arasındaki ilişkiler

    • İç açı ile dış açı, ortak bir kenara sahip olduğu için doğru açı (180°) oluşturur.
    • Bir köşedeki iç açı ne kadar büyükse, o köşedeki dış açı o kadar küçüktür (zıt yönde lineer ilişki).

  2. Üçgenin iç açıları

    • m(A) + m(B) + m(C) = 180° (tüm üçgenler için evrenseldir).

  3. Üçgende dış açı

    • Bir köşedeki dış açı, üçgenin diğer iki iç açısının toplamına da eşittir. Örnek: Dış açı A’, B ve C iç açılarını içeriyorsa, A’ = B + C. Bu özellik de 360° neticesiyle bağlantılı bir başka bakış açısı sağlar.

  4. Dörtgen, beşgen ve diğer çokgenlerin dış açıları

    • Bu teorem, yalnızca üçgenle sınırlı değildir; herhangi bir dış bükey n-genin dış açıları toplamı daima 360°’dir. Üçgen özel durumda n=3 için 360° elde eder.

  5. Üçgende tek köşedeki iç ve dış açılar

    • m(A) + m(A’) = 180° şeklindeki “komşu bütünler (lineer çift) olma” özelliği, doğru üzerindeki açılar için genel bir ilkedir.

5. Sık Yapılan Hatalar

  1. İç açı ile dış açıyı 180° yerine 360° sanmak:
    Öğrenciler bazen “iç açı + dış açı = 360°” diye karıştırabilir. Oysa bir noktanın çevresindeki tam tur (360°) başka bir kavramdır; burada sadece aynı doğru üzerinde duran iki açının ölçüleri 180° olmak zorundadır.

  2. Dış açılar toplamını 180° ile karıştırmak:
    Aslında dış açıların toplamı 360° iken, iç açıların toplamı 180°’dir. İkisi farklı şeylerdir; bu ikisini karıştırmamak önemlidir.

  3. Yanlış köşe seçmek:
    Özellikle sorularda “hangi köşenin dış açısına bakıyoruz” sorusu önemlidir. EBD’nin hangi köşenin dış açısı olduğunun doğru anlaşılması gerekir. Soruda B köşesinde uzatılan kenar aracılığıyla EBD açısı oluşturuluyorsa, bu dış açıdır ve B köşesinin iç açısıyla 180° tamamlar.

  4. X’in doğru yerine konmaması:
    Denklemde x değeri bulunduktan sonra, istenen açı iç mi dış mı dikkatli ayırt etmek gerekir. Yukarıdaki örnekte ABC açısını isterken EBD’nin 120° olması, B açısının ise 60° olması gerektiğini doğru anlamalıyız.

6. Derinlemesine Anlama ve İlaveten Yapılabilecek Alıştırmalar

  • Alıştırma 1: Bir ABC üçgeninde, dış açılarının ölçüleri sırasıyla A’ = 2y + 50°, B’ = 3y – 10°, C’ = 130° olarak verilmiş olsun. Dış açıların toplamının 360° olduğundan hareketle y değerini bulunuz. Ardından, en büyük ve en küçük dış açıları hesaplayınız.

  • Alıştırma 2: Herhangi bir üçgende A, B, C iç açılarının üstel ifadelerle (örneğin A=2k+10°, B=3k-20°, C=4k+30°) verildiği durumlarda:

    1. İç açıların toplamı 180°’yi kullanarak k’yı bulunuz.
    2. Her köşenin dış açısını hesaplayınız.
    3. Bulduğunuz üç dış açıyı toplayarak 360° elde ettiğinizi doğrulayınız.

  • Alıştırma 3 (Zorlayıcı): Bir ABC üçgenini çizin ve A, B, C köşelerinin her birinden birer tane ışın uzatın. Elde ettiğiniz dış açılara A’, B’, C’ deyin. Ardından açı ölçüleri ile oynayarak, dış açıların daima 360° olduğunu ne kadar farklı çizimde doğrulayabildiğinizi gözlemleyin.

Bu tarz ek alıştırmalar sayesinde “dış açılar toplamı = 360°” teoremini daha iyi pekiştirebilirsiniz.

7. Kısa Bir Matematiksel Arkaplan

Matematiksel olarak bir düzlemde nokta, doğru parçası, açı gibi kavramlar, Öklid geometrisinin temelini oluşturur. Üçgenler bu sistemin en temel çokgenleridir. İç açılarının toplamının 180° oluşu, Öklid’in beşinci postülatından (paralellik aksiyomu) kaynaklıdır. Dış açılar toplamının 360° çıkması, bu 180° ilkesinden türetilen bir özelliktir.

Bu “360°” sonucu, pek çok matematik ve mühendislik uygulamasında (çokgenlerin çevresinde gezerken açıların kapadığı alanı hesaplamada, katı cisim modellemelerinde vb.) hayati önem taşır. Üçgensel ağlar (triangulation) kullanarak yüzey modellemeleri yapılırken, her bir üçgenin dış açılarının 360° olması, geometrik tutarlılık açısından kritik bir araçtır.

8. Soruya Dönüş ve Nihai Sonuç

  • Teorem İspatı: “Bir üçgenin dış açılarının toplamı 360°’dir” ifadesi, yukarıdaki gibi adım adım doğrulanarak netleştirildi.
  • Örnek Problem: “ABC üçgeninde m(DAC) = 6x – 20°, m(EBD) = 4x + 40°, m(ACF) = 140° olduğuna göre, ABC açısının ölçüsü nedir?”
    • Dış açıların toplamından x = 20 bulundu.
    • B köşesinin iç açısı (ABC), B’nin dış açısı (EBD = 120°) ile 180° bütün olduğundan 60°’dir.

Bu nedenle, istenen ABC açısı 60° olarak hesaplanmaktadır.

Kısa Özet

  1. Dış açı + İç açı = 180° (Doğrusal çift).
  2. Üç köşedeki (iç + dış) toplamları => 3 × 180° = 540°.
  3. İç açılar 180° olduğundan, geri kalan üç dış açının toplamı 360°’dir.
  4. Örnekteki problemde x=20 hesaplanır, B’nin dış açısı 120° olur; dolayısıyla B’nin iç açısı 60°’dir.

Bu kadarıyla hem teoremi hem de örneği ayrıntılı şekilde çözmüş olduk.

@Melisa18