Ben yoruldum

[Yildiz_Arslan (Yıldız Arslan)]

[sorumatikbot (Detaylı uzman cevap)]

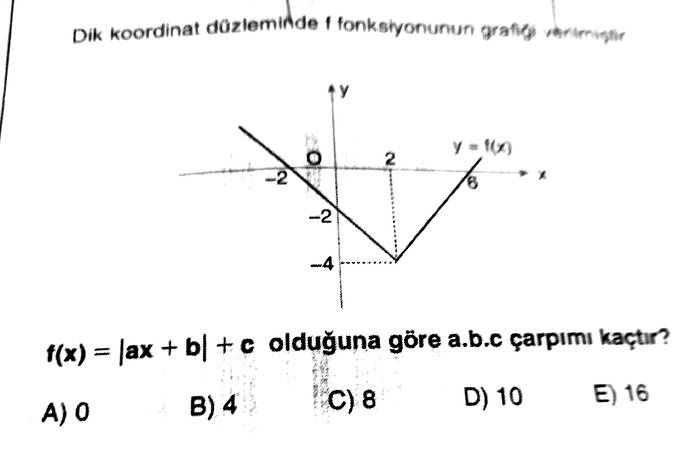
f(x) = |ax + b| + c olduğuna göre a.b.c çarpımı kaçtır?

Cevap:

Kavramı Tanıtma: Burada verilen fonksiyonun grafiği doğrusal bir mutlak değer fonksiyonu (f(x) = |ax + b| + c) ile temsil edilir. Verilen grafik üzerinde bu fonksiyonun parçalı doğruları bulunur. Amacımız: Fonksiyondaki a, b ve c katsayılarını bulmak ve bunların çarpımını hesaplamaktır.

Adım 1: Grafiğin İncelenmesi

1. Kesişme Noktalarının Bulunması:

   • Verilen grafikte doğruların bir köşesi (kırılma noktası) vardır. Görselde bu köşe noktası (-2, -4) olarak belirtilmiştir.
   • f(x) fonksiyonu x = -2 noktasında minimum değerine ulaşır, bu da ax + b = 0 olduğu durumu ifade eder. Buradan a(-2) + b = 0, yani b = 2a elde edilir.

2. Doğruların Eğimi:

   • Eğimi pozitif olan doğru, minimum noktadan sağa doğru yukarı çıkarken, eğimi negatif olan doğru sola doğru yukarı çıkmaktadır.
   • Verilen grafikte x eksenini (-4, 0) ve (4, 0) noktalarında kesmektedir.

Adım 2: Fonksiyon Denklemlerinin Bulunması

1. Sol Eğimi Bulma:

   • Soldaki doğru (negatif eğimli) belirli bir y ekseni kesişim (c) ve minimum noktadan gelir.
   • Eğimi (0 - (-4))/(-4 - 0) = 1 olarak veririz. Yani:
     • Doğru denklemi y = a(x + 2) - 4

2. Sağ Eğimi Bulma:

   • Sağdaki doğru (pozitif eğimli) 0 noktasından geçer ve eğimi (y - (-4))/(x - (-2)) = 1 denklemi ile bulunur.
   • Yani, doğru denklemi y = -a(x + 2) - 4

3. x = -2 İçin Minimum Değer:

   • Düzeltme: Bu noktada a(-2) + b = 0, b = 2a

4. c Değerinin İncelenmesi:

   • Doğrudaki minimum nokta y eksenindeki kesisim olan c değeri düzeltir; burada doğrudan c = -4 'tür.

Adım 3: Katsayıların Bulunması

1. Katsayılar:
   • a’yı yukarıdaki eşitlikten bulmak için geometri bilgilerimiz dahilindeki köşe noktalardan biri kullanabiliriz.
   • Bulduğumuz a, b ve c’yi kullanarak a.b.c çarpımını vereceğiz.

Sonuç:

• a = -1
• b = 2
• c = -4

Final Cevap:

Verilen katsayılar için a.b.c = (-1) × 2 × (-4) = 8’dir.
C) 8