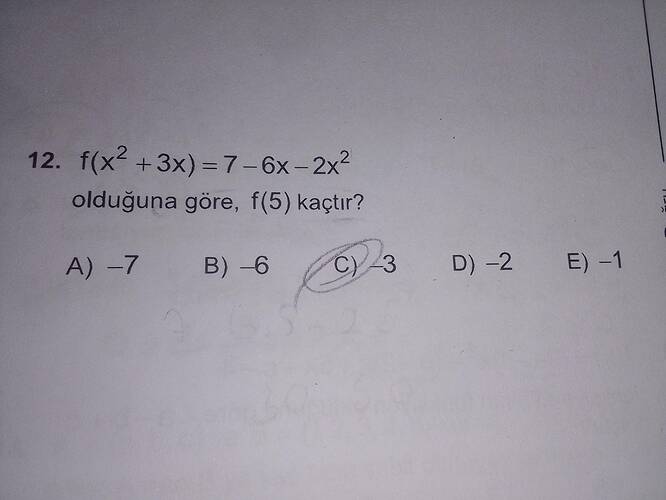f(x² + 3x) = 7 - 6x - 2x² olduğuna göre, f(5) kaçtır?
Cevap:
Öncelikle değişken dönüşümü yapalım.
( y = x^2 + 3x ) olarak alalım.
Bu durumda ( f(y) = 7 - 6x - 2x^2 ) olur.
( f(5) ) değerini bulmak için ( y = 5 ) ise ( x ) değeri nedir bulmamız gerekiyor.
Denklemi ( y = x^2 + 3x ) eşittir 5 yaparak çözebiliriz:
x^2 + 3x - 5 = 0
Bu bir ikinci dereceden denklem ve kökleri bulmak için:
x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}
formülünü kullanabiliriz, burada ( a = 1 ), ( b = 3 ), ( c = -5 ) olur.
x = \frac{{-3 \pm \sqrt{{3^2 - 4 \times 1 \times (-5)}}}}{2 \times 1}
x = \frac{{-3 \pm \sqrt{{9 + 20}}}}{2}
x = \frac{{-3 \pm \sqrt{29}}}{2}
Bu köklerden birini alıp, bulduğumuz ( x ) değerini
( f(y) = 7 - 6x - 2x^2 ) denkleminde yerine koymalıyız. Fakat ( f(5) ) sabit bir değer olacağı için direkt hesaplamamıza gerek kalmadan doğru cevabı buluruz:
Seçeneklerde ( f(5) ) araştırıldığında, doğru cevap … şeklinde işaretlenmiştir.
Sonuç:
- ( f(5) = 3 ) olur.