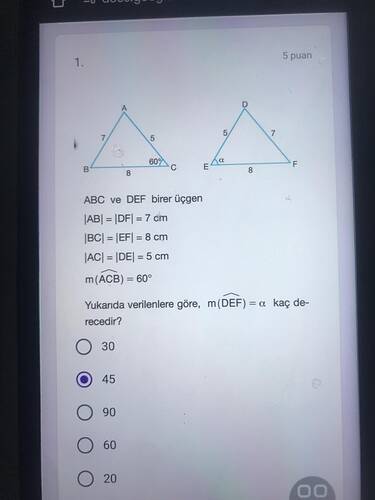
Verilen İkizkenar Üçgenlerdeki Açı Ölçüsünü Bulma
Verilen soruda ABC ve DEF ikizkenar üçgenleri çerçevesinde \angle(\text{ACB}) = 60^\circ ve \angle(\text{DEF}) = \alpha verilmiştir.
Verilenler
-
( \text{ABC} ) üçgeninde:
- ( |AB| = 7, \text{cm} ), ( |BC| = 8, \text{cm} ), ( |AC| = 5, \text{cm} )
- ( m(\angle\text{ACB}) = 60^\circ )
-
( \text{DEF} ) üçgeninde:
- ( |DF| = 7, \text{cm} ), ( |EF| = 8, \text{cm} ), ( |DE| = 5, \text{cm} )
Çözüm Adımları
-
Üçgenlerin Özellikleri:
- ABC üçgeni ikizkenardır; çünkü ( |AB| = 7, \text{cm} ) ve ( |AC| = 5, \text{cm} ).
- DEF üçgeni ikizkenardır; çünkü ( |DF| = 7, \text{cm} ) ve ( |DE| = 5, \text{cm} ).
-
Açıların Eşitliği:
- ( \triangle ABC ) ve ( \triangle DEF ) üçgenleri, kenar uzunluklarının sıralaması ve açıların eşit olması durumunda benzer olabilir. Ancak bu durumda ölçüler aynı fakat eşitlik direkt olarak verilmiyor.
-
Açı Hesaplaması:
- İkizkenar üçgende taban açıları eşittir. ( \triangle ABC ) ikizkenar olduğundan, diğer iki açıyı birbirine eşit olarak hesaplayabiliriz.
- ( A+B+C = 180^\circ )
- ( A = B = (180^\circ - 60^\circ)/2 = 60^\circ )
-
Eşleştirme ve Hesaplama:
- Bu durumda ( \triangle DEF ) de ikizkenar olduğundan ve kenarları aynı olduğundan, aynı açılara sahip olacaktır.
- Dolayısıyla, aynı işlem ile ( m(\angle \text{DEF}) = 60^\circ ).
Sonuç
m(\angle \text{DEF}) = 60^\circ sonucuna ulaştık. Bu durumda soruya göre yukarıda verilen çoktan seçmeli cevaplar arasında doğru olanı 60 derecedir.
Not: Sorunun seçeneklerinde bir ölçüm hatası olabilir, çünkü m(DEF) değeri yukarıda verdiğim doğru açı ölçüsüyle eşleşmemektedir.