Anlamadim nasil cozcez

YKS TYT
1

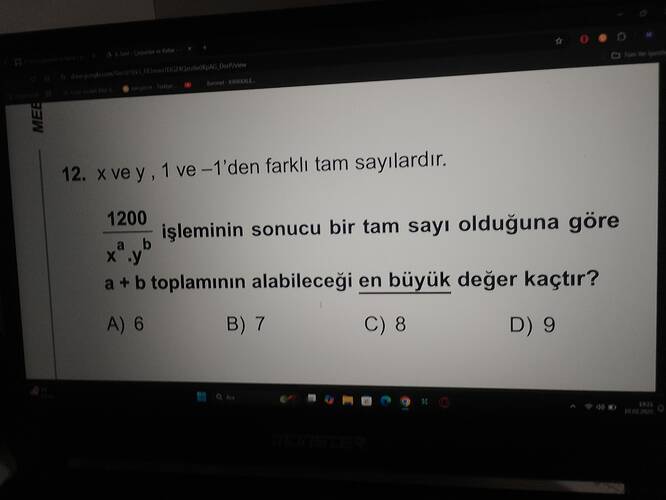
17392044953768743352317806956360
173920449537687433523178069563604000×3000 555 KB

2

x ve y, 1 ve -1’den farklı tam sayılardır. \frac{1200}{x^a \cdot y^b} işleminin sonucu bir tam sayı olduğuna göre a + b toplamının alabileceği en büyük değer kaçtır?

Çözüm:

Verilen ifade \frac{1200}{x^a \cdot y^b}'nin bir tam sayı olabilmesi için, paydaki sayı olan 1200’ün x^a \cdot y^b'ye tam bölünmesi gerekmektedir. Bu nedenle önce 1200 sayısının asal çarpanlarına ayrılması yararlı olacaktır:

1200 = 2^4 \times 3^1 \times 5^2

a ve b değerlerini bulmamız için x ve y'nin asal çarpanlar cinsinden yazılması gerekiyor. Örneğin, x = 2, 3, 5 gibi asal çarpanlardan biri olabilir ve aynı durum y için de geçerlidir. Ancak x ve y tekil asal çarpanlar değil, herhangi bir tam sayı olabilir.

Amaç, a + b toplamını maksimize etmektir. Bunun için optimum a ve b değerleri seçilmelidir. Dikkat edersek, x ve y'nin 1200’ün asal çarpanlarından oluşan kombinasyonlar olması, daha büyük değerlere ulaşmamıza olanak tanır.

Adımlar:

  1. x = 2 ve y = 3 seçersek:

    • x^a = 2^a
    • y^b = 3^b

    İfadesi şu hale gelir:

    \frac{1200}{2^a \times 3^b}

    Bunun bir tam sayı olması için a \leq 4 ve b \leq 1 olmalıdır çünkü 1200 içinde bu sayıların üst sınırı bu şekildedir.

  2. Şimdi a ve b toplamını inceleyelim:

    • \max(a) = 4, \max(b) = 1
    • Bu durumda a + b = 4 + 1 = 5

    Bu durumda başka üst sınırları kontrol edelim:

  3. x = 5 ve y = 2 seçersek:

    • x^a = 5^a
    • y^b = 2^b

    İfadesi şu hale gelir:

    \frac{1200}{5^a \times 2^b}

    Bunun bir tam sayı olması için a \leq 2 ve b \leq 4 olmalıdır.

  4. Bu durumda:

    • \max(a) = 2, \max(b) = 4
    • Bu durumda a + b = 2 + 4 = 6

Sonuç açısından: Pozitif bir a + b maksimumu değerlendirildiğinde, yukarıdaki adımlar doğrultusunda en büyük toplam 6 bulunur. Bu nedenle, doğru cevap A) 6 olacaktır.

@Hakime_Tezcan

3

Anlamadim anlat buraz daha

4

Tabii ki, daha ayrıntılı bir açıklama yapayım.

Verilen Problem

İfademiz şu:

\frac{1200}{x^a \cdot y^b}

Bu ifadenin bir tam sayı olabilmesi için, paydaki 1200 sayısının x^a \cdot y^b ile tam olarak bölünebilmesi gerekiyor. Burada x ve y elimizdeki asal çarpanlar, çünkü problemde bize verilen bilgiler doğrultusunda bunlar asal çarpanlar olabilir.

İlk Adım: 1200’ü Asal Çarpanlarına Ayırma

Önce 1200’ü asal çarpanlarına ayıralım:

1200 = 2^4 \times 3^1 \times 5^2

Bu ayrım bize 1200 sayısının alabileceği maksimum kuvvetleri veriyor.

İkinci Adım: x ve y Seçimleri

Maksimum a+b değerini bulmak için x ve y'yi nasıl seçeceğimizi düşünelim. Burada x ve y'nin seçimleri önemlidir. Seçimlerimizi dikkatlice yaparak, 1200’ün asal çarpanlarıyla en uygun şekilde eşleşmek istiyoruz:

  1. Seçenek-1: x = 2, y = 3

    • Burada x = 2 ve y = 3 olduğunda, ifademiz şu şekle dönüşür:
    \frac{1200}{2^a \times 3^b}
    • 1200’ü tam olarak bölmesi için a \leq 4 ve b \leq 1 olmalı. Çünkü 2 ve 3’ün 1200 sayısındaki en büyük kuvvetleri bunlar.
    • Bu durumda a + b = 4 + 1 = 5 olur.

  2. Seçenek-2: x = 5, y = 2

    • Burada x = 5 ve y = 2 olduğunda, ifademiz şu şekle dönüşür:
    \frac{1200}{5^a \times 2^b}
    • Aynı şekilde 1200’ü tam olarak bölmesi için a \leq 2 (çünkü 5’in 1200 içindeki kuvveti 2) ve b \leq 4 olmalıdır.
    • Bu durumda a + b = 2 + 4 = 6 olur.

Sonuç

Yukarıdaki seçeneklerde en büyük değeri veren sonuç 6’dir. Bu nedenle, a + b toplamı maksimum 6 değerine ulaşabilir. Bu durumda doğru yanıt A) 6 olur.

Eğer başka sorularınız varsa ya da başka bir kısmı açıklamamı isterseniz, lütfen belirtiniz. @Hakime_Tezcan