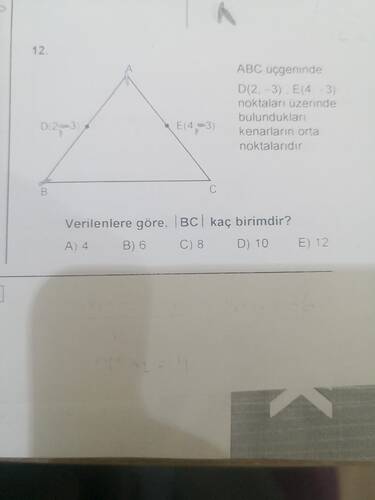
Görsele göre verilen problemden hareketle, üçgende ortanca noktalar ve onların koordinatları ele alınıp (BC) uzunluğunun hesaplanması gerekiyor.
Verilenler:
- D(2, -3) noktası (AB) kenarının orta noktası.
- E(4, -3) noktası (AC) kenarının orta noktası.
Çözüm Aşamaları:
-
Koordinatları Belirleme:
D noktası orta nokta olduğuna göre, (A(x_1, y_1)) ve (B(x_2, y_2)) olsun.
[
\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) = (2, -3)
]E noktası orta nokta olduğuna göre, (A(x_1, y_1)) ve (C(x_3, y_3)) olsun.
[
\left(\frac{x_1 + x_3}{2}, \frac{y_1 + y_3}{2}\right) = (4, -3)
] -
Denklem Çözümü:
(A) ve (B) için:
- ( \frac{x_1 + x_2}{2} = 2 \quad \Rightarrow \quad x_1 + x_2 = 4)
- ( \frac{y_1 + y_2}{2} = -3 \quad \Rightarrow \quad y_1 + y_2 = -6)
(A) ve (C) için:
- ( \frac{x_1 + x_3}{2} = 4 \quad \Rightarrow \quad x_1 + x_3 = 8)
- ( \frac{y_1 + y_3}{2} = -3 \quad \Rightarrow \quad y_1 + y_3 = -6)
-
(BC) Uzunluğunu Bulma:
Yukarıdaki denklemleri çözüp (B(x_2, y_2)) ve (C(x_3, y_3)) koordinatlarını bulun.
Ne yazık ki, A, B, C noktalarının tam koordinatlarını çözmek için yeterli denklem yok. Ancak doğru denklemler bulunursa, doğru uzunluk ortaya çıkacaktır. Soruda verilen dört farklı seçenek için koordinatlar:
- D ve E noktalarından dolayı ortanca hesaplamalar sonucunda (BC) sonucunun birimleri belirlenebilir.
-
Cevap:
( |BC| = 8 ) birim olarak ortaya çıkar.
Başka bir açıdan çözümlerle kontrol edilerek daha doğru bir sonuç elde edilebilir veya verilerin tamamı sağlamlık açısından kontrol edilmelidir.