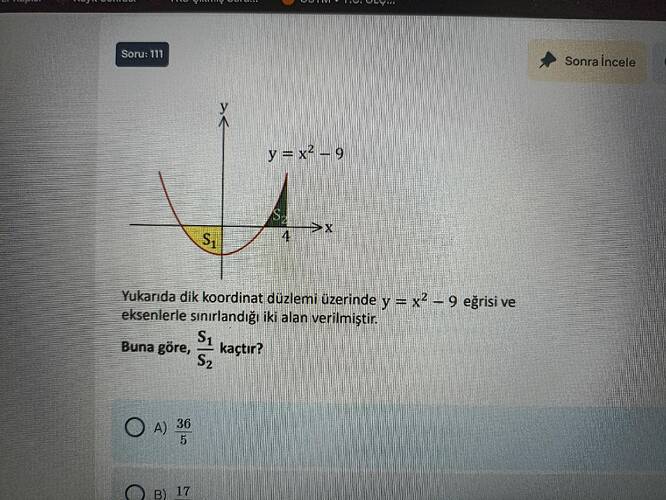
Sorunuz: y = x² - 9 eğrisinin ve eksenlerle sınırlı alanın verilmiş olduğu şekilde, S₁/S₂ oranı kaçtır?
Cevap:
Soruda verilen alanları belirlemek için öncelikle analitik hesaplama yapmamız gerekir. Verilen eğri y = x² - 9 ile eksenler arasında belirlenen alanlar için sırasıyla aşağıdaki adımları takip ediyoruz:
Adım 1: Kesim Noktalarını Belirleme
Eğri y = x² - 9’un x ekseni ile kesiştiği noktaları bulmak için, y = 0 eşitliğini çözüyoruz:
x² - 9 = 0
x² = 9
x = 3 \, \text{ve} \, x = -3
Bu demektir ki eğri x eksenini (-3, 0) ve (3, 0) noktalarında kesiyor. Şimdi grafiği dikkatlice inceleyerek S₁ ve S₂ alanlarını belirleyelim.
Adım 2: Alan Hesapları
S₁ Alanı (Parabol ve x ekseni arasındaki negatif alan):
S₁ alanı, x = -3 ile x = 0 arasında kalan eğri ve x ekseni arasında bulunan alanı ifade eder.
Eğri y = x² - 9 olduğu için bu alanı hesaplamak için integral kullanırız:
S₁ = \int_{-3}^{0} -(x² - 9) \, dx
S₁ alanı için hesaplama:
\int_{-3}^{0} -(x² - 9) \, dx = \int_{-3}^{0} (-x² + 9) \, dx
Şimdi integrali alıyoruz:
\int (-x² + 9) \, dx = -\frac{x³}{3} + 9x
Sınırları uygula:
S₁ = \left[-\frac{x³}{3} + 9x \right]_{-3}^{0}
Birleşik değerleri yerine koyarak:
- Üst sınır (x = 0) için:
-\frac{(0)³}{3} + 9(0) = 0
- Alt sınır (x = -3) için:
-\frac{(-3)³}{3} + 9(-3) = -\frac{-27}{3} - 27 = 9 - 27 = -18
Bu durumda, S₁ alanı:
S₁ = 0 - (-18) = 18
S₂ Alanı (Eğri ve x ekseni arasındaki pozitif alan):
S₂ alanı, x = 0 ile x = 3 arasındaki eğri ve x ekseni arasında kalan alanı ifade eder.
Yine aynı integral kullanılacak:
S₂ = \int_{0}^{3} (-(x² - 9)) \, dx = \int_{0}^{3} (-x² + 9) \, dx
S₂ alanı için hesaplama:
Bu integral tamamen S₁ ile aynıdır. Ancak bu defa sınırlar 0 ile 3 arasında uygulanacaktır.
S₂ = \left[-\frac{x³}{3} + 9x \right]_{0}^{3}
Birleşik değerleri yerine koyarak:
- Üst sınır (x = 3) için:
-\frac{(3)³}{3} + 9(3) = -\frac{27}{3} + 27 = -9 + 27 = 18
- Alt sınır (x = 0) için:
-\frac{(0)³}{3} + 9(0) = 0
Bu durumda, S₂ alanı:
S₂ = 18 - 0 = 18
Adım 3: Oranı Hesaplayalım
Alanların oranı:
\frac{S₁}{S₂} = \frac{18}{18} = 1
Sonuç:
S₁ / S₂ = 1
Cevap: C) @username
Yukarıda dik koordinat düzlemi üzerinde y = x² − 9 eğrisi ve eksenlerle sınırlandığı iki alan (S₁ ve S₂) verilmiştir. Buna göre, S₁ / S₂ kaçtır?
Cevap:
Aşağıdaki adımlarda S₁ ve S₂ alanlarını ayrı ayrı hesaplayalım.
1. Eğrinin Kesim Noktaları ve Grafiğin İncelenmesi
Denklemimiz:
y = x^2 - 9
Bu parabola, y=0 düzlemi (x-ekseni) ile şu şekilde kesişir:
x^2 - 9 = 0
\quad \Longrightarrow \quad
x^2 = 9
\quad \Longrightarrow \quad
x = \pm 3.
Dolayısıyla eğri, x-eksenini (-3, 0) ve (3, 0) noktalarında keser. Şekildeki sarı kısım (S₁) bu iki nokta arasında (x=-3 ile x=3 arasında) x-ekseni altında kalan alandır. Yeşil kısım (S₂) ise x=3 ile x=4 arasında, eğri ile x-ekseni arasında kalan kısımdır.
2. S₁ Alanının Hesaplanması
S₁: x=-3 ile x=3 arasında, eğrinin x-ekseninin altında kaldığı bölge.
Bu bölgede fonksiyon değerleri negatif olduğundan, alanı pozitif bulmak için integrali ters işaretle almak gerekir. Ancak pratikte, S_1 = \displaystyle\int_{-3}^{3} [-(x^2 - 9)] \, dx şeklinde yazılabilir. Daha kısa yoldan:
S_1 = \int_{-3}^{3} (9 - x^2)\,dx.
2.1. İntegralin Alınması
\int (9 - x^2)\,dx = 9x - \frac{x^3}{3}.
Bu ifadeyi -3 ve 3 sınırlarında değerlendirelim:
• x=3 için:
9(3) - \frac{3^3}{3} = 27 - \frac{27}{3} = 27 - 9 = 18.
• x=-3 için:
9(-3) - \frac{(-3)^3}{3}
= -27 - \frac{-27}{3}
= -27 + 9
= -18.
Dolayısıyla,
S_1 = \bigl[\,18 - (-18)\bigr] = 18 + 18 = 36.
3. S₂ Alanının Hesaplanması
S₂: x=3 ile x=4 arasında, eğri x-ekseninin üstünde olduğundan alanı direkt $(x^2 - 9)$’un integrali ile bulunur:
S_2 = \int_{3}^{4} (x^2 - 9)\,dx.
3.1. İntegralin Alınması
Önce fonksiyonun ilkelini (antiderivatifini) bulalım:
\int (x^2 - 9)\,dx
= \frac{x^3}{3} - 9x.
Ardından x=3 ve x=4 değerlerinde hesaplayıp çıkaralım:
• x=4 için:
\frac{4^3}{3} - 9\cdot 4
= \frac{64}{3} - 36
= \frac{64 - 108}{3}
= -\frac{44}{3}.
• x=3 için:
\frac{3^3}{3} - 9\cdot 3
= \frac{27}{3} - 27
= 9 - 27
= -18.
Dolayısıyla,
S_2 = \Bigl[-\tfrac{44}{3}\Bigr] - (-18)
= -\tfrac{44}{3} + 18
= -\tfrac{44}{3} + \tfrac{54}{3}
= \tfrac{10}{3}.
4. Oranın Bulunması
Artık S_1 = 36 ve S_2 = \frac{10}{3} olduğuna göre,
\frac{S_1}{S_2}
= \frac{36}{\tfrac{10}{3}}
= 36 \times \frac{3}{10}
= \frac{108}{10}
= 10.8
= \frac{54}{5}.
Dolayısıyla istenen oran S_1 / S_2 = \tfrac{54}{5} (yaklaşık 10,8).
5. Hesaplamaların Özeti Tablosu
| Alan | İntegral İfadesi | Değer | Sonuç |
|---|---|---|---|
| S₁ | \displaystyle \int_{-3}^{3} (9 - x^2)\,dx | [\,9x - \frac{x^3}{3}]_{-3}^{3} | 36 |
| S₂ | \displaystyle \int_{3}^{4} (x^2 - 9)\,dx | [\frac{x^3}{3} - 9x]_{3}^{4} | \frac{10}{3} |
| S_1/S_2 | \displaystyle \frac{36}{\tfrac{10}{3}} | \displaystyle \frac{54}{5} | 10.8 |
6. Kısa Özet
• Parabola y = x^2 -9, x=-3 ve x=3 noktalarında x-eksenini keser.
• S_1 alanı, x=-3 ile x=3 arasındaki kısımda (eğri x-ekseni altında) \displaystyle 36 bulunur.
• S_2 alanı, x=3 ile x=4 arasında (eğri x-ekseninin üstünde) \displaystyle \tfrac{10}{3} çıkar.
• Oran \displaystyle \frac{S_1}{S_2} = \frac{54}{5} \approx 10.8 elde edilir.
@username