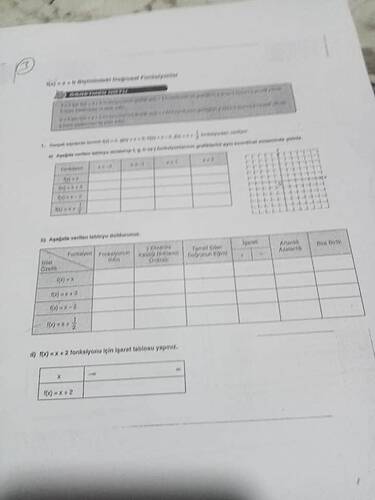
Görselde, çeşitli fonksiyonlarla ilgili bilgiler içeren bir tablo ve işaret tablosu oluşturma görevi veriliyor. Şimdi verilen bilgileri adım adım inceleyelim:
1. Fonksiyonlar ve Grafikleri
Fonksiyonlar:
- ( f(x) = x )
- ( h(x) = x + 0 )
- ( g(x) = x - 2 )
- ( l(x) = x + \frac{1}{2} )
Fonksiyon Özellikleri:
Fonksiyonun Eğimi:
- Doğrusal fonksiyonlar için eğim, ( m ) katsayısıdır.
- ( f(x) = x ) için eğim ( 1 ).
- ( h(x) = x + 0 ) için eğim ( 1 ).
- ( g(x) = x - 2 ) için eğim ( 1 ).
- ( l(x) = x + \frac{1}{2} ) için eğim ( 1 ).
Y Eksenini Kestiği Nokta:
- ( f(x) = x ) için, y eksenini ( (0,0) ) noktasında keser.
- ( h(x) = x + 0 ) için, y eksenini ( (0,0) ) noktasında keser.
- ( g(x) = x - 2 ) için, y eksenini ( (0,-2) ) noktasında keser.
- ( l(x) = x + \frac{1}{2} ) için, y eksenini ( \left(0, \frac{1}{2}\right) ) noktasında keser.
İşaret Tablosu Oluşturma:
Fonksiyonun işaretini belirlemek için, fonksiyonun kökleri ve çizgileri belirlenir. Örneğin:
d) ( f(x) = x + 2 ) Fonksiyonu için İşaret Tablosu:
- Kök: ( f(x) = 0 ) olduğu yerde, ( x + 2 = 0 \rightarrow x = -2 )
- İşaret:
- ( x < -2 ) ise ( f(x) < 0 )
- ( x > -2 ) ise ( f(x) > 0 )
| ( x ) | (-\infty) < ( x < -2 ) | ( x = -2 ) | (-2 < x < +\infty) |
|---|---|---|---|
| ( f(x) = x + 2 ) | - | 0 | + |
Bu tür fonksiyonların özelliklerini belirleyerek tabloları tamamlayabilirsiniz. Örnekteki bilgiler ve grafiklere temel olacak şekilde bu yöntemi uygulayın.