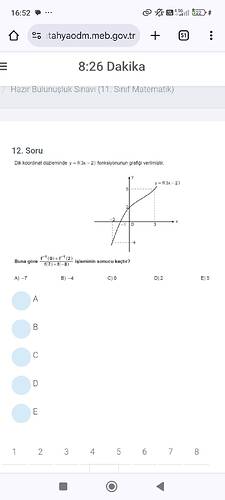
Dik koordinat düzleminde ( y = f(3x - 2) ) fonksiyonunun grafiği verilmiştir. Buna göre (\frac{f^{-1}(0) + f^{-1}(2)}{f(7) + f(-8)}) işleminin sonucu kaçtır?
Cevap:
Soruda verilen grafikteki bilgileri çözüme uygulayarak ilerleyelim.
Çözüm Adımları:
-
Ters Fonksiyon Değerlerini Bulma:
- ( f^{-1}(0) ) değeri: Grafikten ( y = 0 ) iken ( x ) değerini bulmamız gerekir. Grafikten bakıldığında ( y = 0 ) için ( x = 2 ) olduğu görülür.
- ( f^{-1}(2) ) değeri: Grafikten ( y = 2 ) iken ( x ) değerini bulmamız gerekir. Grafikten bakıldığında ( y = 2 ) için ( x = 3 ) olduğu görülür.
- Bu durumda, ( f^{-1}(0) = 2 ) ve ( f^{-1}(2) = 3 ).
-
Fonksiyon Değerlerini Bulma:
-
( f(7) ): ( 3x - 2 = 7 ) olduğunda ( x )'i bulalım.
3x - 2 = 7 \implies 3x = 9 \implies x = 3Grafikten ( x = 3 ) için ( y = 2 ) olduğu görülür. O halde ( f(7) = 2 ).
-
( f(-8) ): ( 3x - 2 = -8 ) olduğunda ( x )'i bulalım.
3x - 2 = -8 \implies 3x = -6 \implies x = -2Grafikten ( x = -2 ) için ( y = -4 ) olduğu görülür. O halde ( f(-8) = -4 ).
-
-
İşlemi Hesaplama:
-
Denklem:
\frac{f^{-1}(0) + f^{-1}(2)}{f(7) + f(-8)} = \frac{2 + 3}{2 + (-4)} -
Hesaplama:
\frac{5}{-2} = -\frac{5}{2}
-
Verilen işlemin sonucu (-\frac{5}{2})'dir. Ancak seçenekler arasında bu doğrudan verilmeyen bir tabandır. Hatalı bir soru olabilir ya da seçeneklerin güncellenmesi gerekebilir.