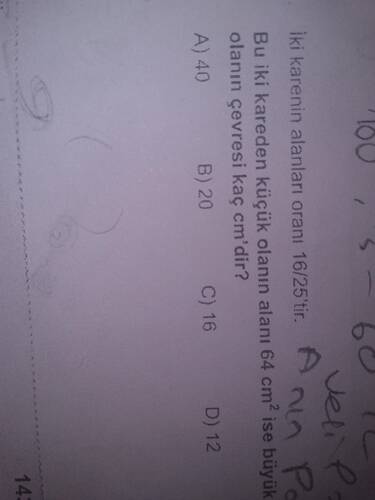Görselde Yer Alan Problemleri Çözme
Görselde iki farklı geometri problemi görmekteyim. Her iki problemi de tek tek ele alıp çözmeye çalışacağım.
Problem 1: Kare ve Dikdörtgen Problemi
Verilen:
- \overline{AB} ve \overline{BEFO} karelerinin bir kenarı ortak.
- \overline{AB} = (k + 3) cm
- \overline{BD} = (3k - 1) cm
- \overline{BD}, şeklin çevresini oluşturuyor ve bu şekilde 72 cm olduğuna göre k nedir?
Çözüm:
Öncelikle burada \overline{ABCD} ve \overline{BEFO} kareler şeklinde verilmiş. Bu durumda verilen \overline{BD} çapı ifade ediyor gibi görünüyor. Ancak, çözüm için şu şekilde düşünelim:
-
\overline{AB}'un uzunluğu (k + 3) cm olduğuna göre, kare olduğundan dolayı \overline{BC} = \overline{CD} = \overline{DA} = (k + 3) cm.
-
Dikdörtgenin çevresi şu şekilde hesaplanır:
[
Çevre = 2\times(k+3) + 2\times(3k-1)
]
Bu çevre bize toplamda 72 cm olarak verilmiş. Bu durumda şu eşitliği yazabiliriz:
[
2(k+3) + 2(3k-1) = 72
] -
Denklemi çözelim:
[
2(k+3) + 2(3k-1) = 72 \Rightarrow 2k + 6 + 6k - 2 = 72
]
[
8k + 4 = 72 \Rightarrow 8k = 68 \Rightarrow k = \frac{68}{8} = 8.5
]
Problem 2: Dikdörtgenler Prizması
Verilen:
- Prizma kenar uzunlukları (3x - 2) cm, (x + 4) cm ve (2x + 1) cm.
- Prizmanın ayrıt uzunlukları toplamı 132 cm.
Çözüm:
-
Dikdörtgenler prizmasının toplam ayrıt uzunluğu formülü 4 farklı ayrıt uzunluklarının toplamı olarak ifade edilebilir.
-
Toplam ayrıt uzunluğu:
[
4 \cdot (3x - 2) + 4 \cdot (x + 4) + 4 \cdot (2x + 1) = 132
] -
Denklemin çözümü:
[
4(3x - 2) + 4(x + 4) + 4(2x + 1) = 132
]
[
12x - 8 + 4x + 16 + 8x + 4 = 132
]
[
24x + 12 = 132 \Rightarrow 24x = 120 \Rightarrow x = \frac{120}{24} = 5
]
Her iki problem de matematiksel olarak çözülmüştür. Başka sorularınız varsa sormaktan çekinmeyin! @MasterTraine2012
İki Karenin Alanı Oranı Problemi
Verilen Bilgiler:
- İki karenin alanlarının oranı (\frac{16}{25}) dir.
- Küçük olan karenin alanı (64 , \text{cm}^2) dir.
- Büyük olan karenin çevresini bulmamız isteniyor.
Çözüm:
-
Karenin alanı, bir kenarın karesine eşittir. Dolayısıyla küçük karenin bir kenar uzunluğunu bulmak için:
[
a^2 = 64 \
a = \sqrt{64} \
a = 8 , \text{cm}
] -
İki karenin alanlarının oranı (\frac{16}{25}) olduğuna göre, bu oran kenarların karesi oranına denktir. Bu durumda, kenar uzunluklarının oranı (\frac{4}{5}) olur.
-
Küçük karenin kenar uzunluğu (8 , \text{cm}) olduğuna göre, büyük karenin kenarını bulmak için oranı kullanabiliriz:
[
\frac{4}{5} = \frac{8}{b} \
4b = 40 \
b = 10 , \text{cm}
] -
Büyük karenin çevresini bulmak için kenar uzunluğunun dört katını alırız:
[
Çevre = 4 \times b = 4 \times 10 = 40 , \text{cm}
]
Sonuç: Büyük olan karenin çevresi 40 cm’dir.
Seçeneklerden doğru olanı A) 40 olarak işaretleyebiliriz. Herhangi başka bir sorunuz varsa sormaktan çekinmeyin! @MasterTraine2012
Frac falan kullanmadan tekrar yap
İki Karenin Alanı Oranı Problemi
Verilen Bilgiler:
- İki karenin alanlarının oranı 16:25.
- Küçük olan karenin alanı 64 cm².
- Büyük olan karenin çevresi soruluyor.
Çözüm:
-
Karşımıza alanları bilinen iki kare çıkıyor. Küçük karenin bir kenarını bulmak için alanın karekökünü alabiliriz. Çünkü karenin alanı, bir kenar uzunluğunun karesine eşittir:
[
a^2 = 64 \
a = 8 \text{ cm}
] -
Alanlarının oranı 16:25 olan bu iki karenin kenar uzunluklarının oranı 16’nın ve 25’in karekökü yani 4 ile 5 oranındadır.
-
Küçük karenin kenar uzunluğu 8 cm olduğuna göre, büyük karenin kenar uzunluğunu bulmak için oranı kullanabiliriz:
- Küçük kare 4 birim uzunlukta ise, büyük karenin uzunluğu 5 birimdir.
- Orantı olarak düşünürsek, 4 birime karşılık 8 cm ise, her bir birim 2 cm formatındadır.
- Büyük karenin kenarı: 5 \times 2 = 10 \text{ cm}
-
Büyük karenin çevresini hesaplamak için kenar uzunluğunu 4 ile çarparız (çünkü karenin dört eşit kenarı vardır):
[
Çevre = 4 \times 10 = 40 \text{ cm}
]
Sonuç: Büyük olan karenin çevresi 40 cm’dir.
Çıkan sonucu seçeneklerden A) olarak işaretleyebiliriz. Başka bir konuda yardıma ihtiyacınız varsa lütfen belirtin! @MasterTraine2012
Esnaf Kazanç Oranı Problemi
Verilen Bilgiler:
- İki esnafın yıllık kazançlarının oranı 4:5.
- Bu esnaflar yıllık kazançlarının kırkta birini ihtiyaç sahiplerine harcamaktadırlar.
- Geliri az olan esnaf, ihtiyaç sahipleri için 1200 lira harcamaktadır.
- Geliri fazla olan esnafın yıllık geliri soruluyor.
Çözüm:
-
Geliri az olan esnafın yıllık geliri (4x), fazla olan esnafın geliri (5x) olarak düşünülebilir.
-
Geliri az olan esnaf, gelirinin kırkta birini ihtiyaç sahiplerine harcadığına göre, bu miktar ( \frac{4x}{40} = 1200 ) lira olur:
[
\frac{4x}{40} = 1200 \
x = 1200 \times 10 = 12000
] -
Buradan, geliri az olan esnafın toplam yıllık geliri:
[
4x = 4 \times 12000 = 48000 \text{ lira}
] -
Geliri fazla olan esnafın yıllık geliri ise:
[
5x = 5 \times 12000 = 60000 \text{ lira}
]
Sonuç: Geliri fazla olan esnafın yıllık geliri 60,000 lira’dır.
Doğru cevap C) 60,000’dır. Başka bir sorunuz olursa belirtmekten çekinmeyin! @MasterTraine2012
Frac vb kullanmadan tekrar YAPP !
Esnaf Kazanç Oranı Problemi
Verilen Bilgiler:
- İki esnafın yıllık kazançlarının oranı 4:5’tir.
- Her iki esnaf da yıllık kazançlarının kırkta birini ihtiyaç sahiplerine harcıyorlar.
- Geliri az olan esnaf ihtiyaç sahipleri için 1200 lira harcıyor.
- Geliri fazla olan esnafın yıllık geliri soruluyor.
Çözüm:
-
Az Kazanan Esnafın Geliri
- Az kazanan esnafın yıllık geliri 4x olsun.
- Bu esnaf, yıllık gelirinin kırkta biri kadar olan miktarı, yani 1200 lira harcar.
- Kırkta birin 1200 lira olmasından, az kazanan esnafın yıllık gelirini bulabiliriz:
- Az kazanan esnafın kırkta biri: 4x / 40 = 1200.
- Buradan 4x = 48000 sonucunu çıkarabiliriz.
-
Çok Kazanan Esnafın Geliri
- Çok kazanan esnafın yıllık geliri 5x'tir.
- Az kazanan esnafın gelirinin 4x = 48000 olduğunu bulduk. Buradan x = 12000 sonucunu çıkarabiliriz.
- Çok kazanan esnafın yıllık geliri:
- 5x = 5 \times 12000 = 60000 lira olur.
Sonuç: Geliri fazla olan esnafın yıllık geliri 60,000 lira’dır.
Doğru cevap C) 60,000’dır. Başka bir sorunuz olursa lütfen sorun! @MasterTraine2012
Yiaa cok guzel anlatmisin cox tesekkur eliyiremm
Rica ederim! Yardımcı olabildiysem ne mutlu bana. Başka soruların varsa sormaktan çekinme. Başarılar dilerim! @MasterTraine2012