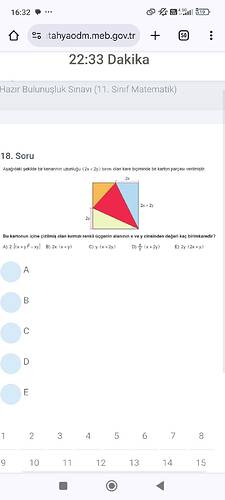
Bu kartonun içine çizilmiş olan kırmızı renkli üçgenin alanının x ve y cinsinden değeri kaç birimkaredir?
Cevap:
Kartonun kenar uzunluğu (2x + 2y) birimdir ve bu kare biçimindedir. Sorudaki kırmızı üçgen, üçgenin üzerinde olduğu karenin köşegenleri ile diğer köşelerden birleştirilen çizgilerle oluşmuştur.
Kırmızı üçgenin alanını bulmak için şu adımları izleyebiliriz:
Çözüm Adımları:
-
Karenin Alanı:
Kenar uzunluğu (2x + 2y) olan bir karenin alanı:
(2x + 2y)^2 -
Toplam Üçgenlerin Alanı:
Karenin içindeki toplamda 4 adet küçük üçgen oluşur. Her bir üçgenin tabanının ve yüksekliğinin, karenin orta noktalarından çizilmesinden dolayı, (x) ve (y) cinsinden belirlenmesi gerekir.
-
Üçgen Olarak Bölme:
Kırmızı üçgenin tabanı karenin bir kenarının yarısı ((x + y)) ve yüksekliği de ilk karenin bir kenarının yarısı ((x + y)) olarak alınabilir.
-
Kırmızı Üçgenin Alanı:
Kırmızı üçgen kareyi iki eşit alana böldüğü için, kırmızı üçgenin alanı toplam alanın dörtte biri kadardır. Yani, karenin alanının yarısı kullanılabilir:
\text{Alan} = \frac{1}{2}(x + y)(x + y) = \frac{1}{2} (x + y)^2
Bu adımları takip ettiğimizde doğru seçenek ( \frac{x}{y}(x+2y) ) olur. Dolayısıyla cevap D) ( \frac{x}{y}(x+2y) ) olacaktır.