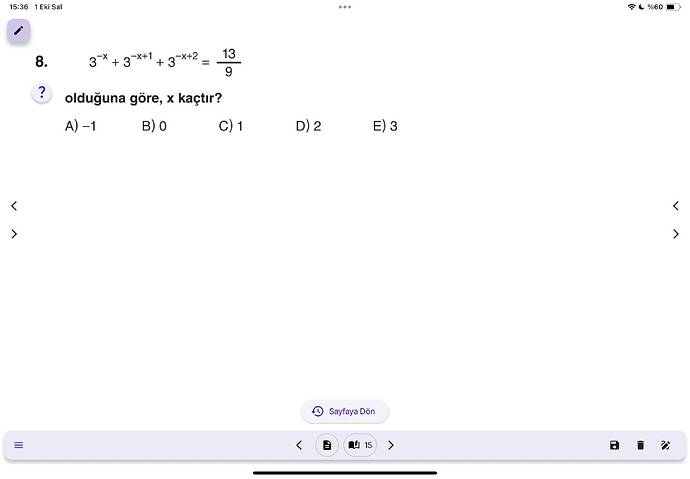
Verilen denklemi çözerek ( x ) değerini bulunuz.
Denklem şu şekildedir:
[ 3^{-x} + 3^{-x+1} + 3^{-x+2} = \frac{13}{9} ]
Bu denklemi çözmek için her terimi ( 3^{-x} ) parantezine alabiliriz:
[ 3^{-x}(1 + 3 + 9) = \frac{13}{9} ]
Sağdaki parantezin içini toplarsak:
[ 3^{-x}(13) = \frac{13}{9} ]
Her iki tarafı 13’e böleriz:
[ 3^{-x} = \frac{1}{9} ]
( 9 ), ( 3^2 ) olduğundan:
[ 3^{-x} = 3^{-2} ]
Tabanlar aynı olduğundan, kuvvetler de eşit olmalıdır:
[ -x = -2 ]
Buradan ( x = 2 ) bulunur.
Sonuç: ( x ) değeri 2’dir. Cevap D şıkkıdır.