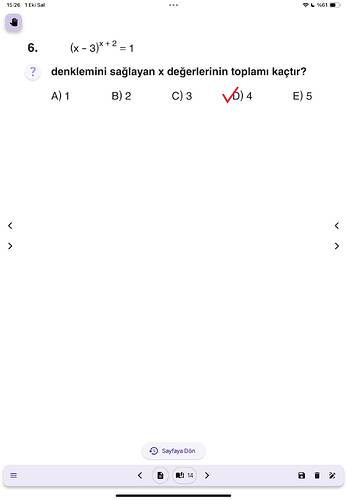
Denklemi sağlayan x değerlerinin toplamı kaçtır?
Cevap:
Verilen denklem:
$$(x-3)^{x+2} = 1$$
Bu denklemin sağlanabilmesi için iki durum söz konusu olabilir:
- Taban 1 olabilir:
(x-3) = 1 \implies x = 4
- Üs 0 olabilir, ve bu sırada taban 0^0 formunu sağlamayacak şekilde 1’den farklı olabilir veya taban -1 olabilir:
- (x+2) = 0 \implies x = -2
Ancak, ikinci durumda (x-3) = -1 olduğundan dolayı (x+2) = 0 için sağlamayacaktır.
Sonuçta, denklemi sağlayan x değerleri x = 4 ve x = -2'dir.
Bu değerlerin toplamı:
$$4 + (-2) = 2$$
Özet: Denklemde sağlanan x değerlerinin toplamı 2’dir.
1 Beğeni