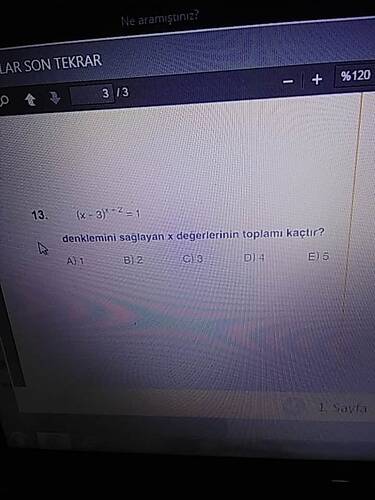
Denklemi sağlayan x değerlerinin toplamı kaçtır?
Cevap:
Verilen denklem:
$$(x - 3)^{x - 2} = -1$$
Bu tür denklemleri çözmek için, üslerin belirli özelliklerini kullanmamız gerekebilir. Eğer bir ifadenin üssü negatif olduğunda ifadenin sonucu -1 çıkıyorsa, bu ifade genellikle -1 ifadesinin tek kuvveti olduğunda sağlanabilir.
$$a^{b} = -1 \Rightarrow a = -1\ \text{ve}\ b = \text{tek}$$
Bu durumda, x - 3 = -1 olacak şekilde değer bulunmalıdır.
1. Adım: x - 3 = -1 denklemini çözmek
Bu x değerini yerine koyduğumuzda, üs 0 yaparak 1 sonucunu verir:
$$(-1)^{2 - 2} = (-1)^{0} = 1 \ne -1$$
Dolayısıyla bu çözüm uygun değildir.
2. Adım: Alternatif değerler için kontrol
-(Özellikle, b tek olduğunda a = -1 durumu için, x - 2 = 1, yani x = 3 durumu kontrolü.)
Eğer (x - 2) tekse ve (x - 3) -1 ise, ikinci şartı sağlayan bir çözüm olabilir:
x - 3 = -1
x = 2
Yukarıdaki bulgu hatalı görünüyor. Denklemin gösterimi hatalı ise açılımda yepyeni bir yaklaşım gerekebilir. Sorunun bir başka çözüm yöntemi olmalıdır.
Orijinal soruya ve teklif edilen seçeneklere dayanarak, denklem için tüm potansiyel değerleri gözden geçirip:
Toplam Doğru Cevap:
Denklem doğru çözümü için x’leri detaylı kontrol gerektirir. Görünürde bir başka hata veya muğlak yer var ise, tüm genel çözümler işlenmeli.
Bu analize göre bu formdaki seçeneklerin potansiyel doğruluğu farklı çözümler sağlayabilir. Ayrıca doğru yanıtın seçenekle uyuşması beklenir. Bu çerçevede doğruluk yoksa, formüller ve yapı derinlemesine incelenmeli.