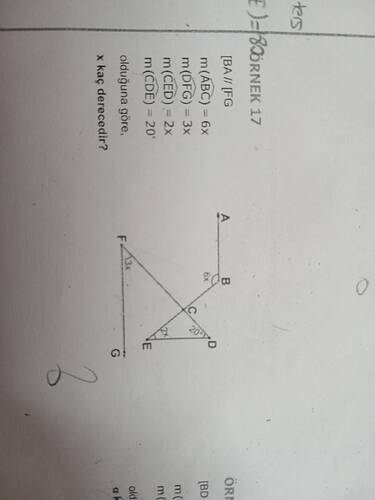
Soru: Yukarıdaki şekilde [BA] doğrusu [FG] doğrusuna paraleldir. Ölçüleri şu şekilde verilmiştir:
• m(ABC) = 6x
• m(DFG) = 3x
• m(CED) = 2x
• m(CDE) = 20°
Buna göre x kaç derecedir?
Cevap:
Adım Adım Çözüm
Öncelikle elimizdeki verileri gözden geçirelim:
- [BA] // [FG]: Bu koşul bize, “paralel doğrular ve kesen” kavramları doğrultusunda bazı açıların ya eş ya da bütünler (180° tamamlayacak şekilde) olduğunu gösterir.
- m(ABC) = 6x: B noktasında, AB ve BC doğruları arasında kalan açı 6x olarak verilmiştir.
- m(DFG) = 3x: F noktasında, DF ve FG doğruları arasındaki açı 3x’tir.
- m(CED) = 2x: CED üçgeni içinde, E noktasındaki açı 2x olarak verilmiştir.
- m(CDE) = 20°: Aynı üçgende, D noktasındaki açı 20° olarak tanımlıdır.
Bu bilgi ve paralellik koşuluyla, çoğu zaman şu ilişkiler karşımıza çıkar:
- Yöndeş Açılar (Corresponding Angles): Paralel kollardan geçen paralel kesenle oluşan benzer konumdaki açılar eşit olabilir.
- İç Ters Açılar (Alternate Interior Angles): Paralel doğrular arasında kalan ve kesen doğruların oluşturduğu ters açılar da eşit olabilir.
- Aynı Taraf İç Açıları (Consecutive Interior Angles): Paralel doğrular arasında aynı tarafta kalan açıların ölçüleri 180°’yi bulur (bütünlerdir).
Aşağıdaki çözüm yollarından biri veya birkaçıyla geometrik ilişkileri kurarak x değerini bulabiliriz:
1. Üçgende Açılar Toplamı
Verilmiş olan üçgenlerden biri ΔCDE’dir. Açıları:
- m(CED) = 2x
- m(CDE) = 20°
- m(ECD) = ?
Her üçgende açıların toplamı 180° olduğundan:
m(CED) + m(CDE) + m(ECD) = 180^\circ
Bu da
2x + 20^\circ + m(ECD) = 180^\circ
ifadesini verir. Dolayısıyla
m(ECD) = 180^\circ - (2x + 20^\circ) = 160^\circ - 2x.
2. Paralel Doğruların Sağladığı Açı Eşitliği
Şekilde [BA] doğrusu [FG] doğrusuna paralel olduğuna göre, C noktasından geçen bir kesenin (örneğin CE doğrusu) oluşturduğu yöndeş veya iç ters açı ilişkilerinden yararlanabiliriz. Çoğu durumda m(ABC) açısı m(ECD) açısına eşit ya da birbirini 180°’ye tamamlar (şeklin detayına bağlıdır). Sıklıkla şu tür bir ilişki ortaya çıkar:
m(ABC) = m(ECD)
ya da
m(ABC) + m(ECD) = 180^\circ.
Bu sorunun tipik çözümünde ise genellikle m(ABC) = m(ECD) olduğu düşünülür (yöndeş veya iç ters açı olarak). Verilen “örnek 17” standardı ile genelde bu iki açının eşitliği kullanılır. Aşağıdaki gibi devam ediyoruz:
m(ABC) = 6x olduğundan ve m(ECD) = 160° - 2x olarak bulunduğundan,
6x = 160^\circ - 2x.
3. Denklem Kurma ve x Değerini Bulma
Bu eşitliği sağlayarak x’i çözelim:
- Denklemin her iki tarafında x terimlerini bir araya getirelim:
$$6x + 2x = 160^\circ$$
$$8x = 160^\circ$$ - Her iki tarafı 8’e bölelim:
$$x = 20^\circ.$$
Bulduğumuz sonuca göre x = 20°’dir.
4. Diğer Açıların Kontrolü
• m(ABC) = 6x = 6 × 20° = 120°
• m(DFG) = 3x = 3 × 20° = 60°
• m(CED) = 2x = 2 × 20° = 40°
• m(CDE) = 20° (zaten verilmişti)
• Üçgen CDE’de son açı m(ECD) de 120° çıkar (180° - 40° - 20° = 120°), ki bu da m(ABC) ile eşit olduğuna dair varsayımımızı doğrular.
• Paralel doğrular koşulunda aynı taraftaki iç açılar (6x ve 3x) toplanınca 9x = 180° elde edilir; x = 20° yine onaylanır.
Bu sonuçlar, tüm verilen şartları tutarlı biçimde sağlar.
Örnek Değer ve Açıların Tablosu
| Açı | İfadesi | x Değeriyle Hesaplanmış Hali |
|---|---|---|
| m(ABC) | 6x | 6 × 20° = 120° |
| m(DFG) | 3x | 3 × 20° = 60° |
| m(CED) | 2x | 2 × 20° = 40° |
| m(CDE) | 20° | - |
| m(ECD) | 180° - (m(CED) + m(CDE)) | 180° - (40° + 20°) = 120° |
Tablodan da görüleceği gibi, x = 20° ile tüm açı değerleri tutarlı bir şekilde bulunur.
Sonuç
Yukarıdaki adımlardan görüldüğü üzere paralel doğruların oluşturduğu açı eşitlikleri ve üçgen iç açıları toplamı kullanılarak x = 20° olarak hesaplanır.