1. Sorunun Doğru/Yanlış Cevapları
I. İki pozitif tam sayının çarpımı pozitif bir tam sayıdır.
- Doğru (D)
II. Zıt işaretli iki tam sayının çarpımı pozitif bir tam sayıdır.
- Yanlış (Y)
- Zıt işaretli sayıların çarpımı negatif olur.
III. Bir tam sayı -1 ile çarpıldığında, çarpım o tam sayının zıt işaretlisi olur.
- Doğru (D)
IV. Çarpma işleminin etkisiz elemanı 0’dır.
- Yanlış (Y)
- Çarpma işleminin etkisiz elemanı 1’dir, 0 etkisiz eleman değildir.
V. Çarpma işleminin değişme özelliği yoktur.
- Yanlış (Y)
- Çarpma işlemi değişme özelliğine sahiptir. (Örneğin: a \times b = b \times a)
2. İşlem: (6 \cdot (-2))
[
6 \times (-2) = -12
]
Sonuç: -12
3. İşlem: (-2 \cdot (2+2))
Öncelikle parantez içini hesaplayalım:
[
2 + 2 = 4
]
Ardından çarpma işlemi:
[
-2 \times 4 = -8
]
Sonuç: -8
4. İşlem: (158 \cdot (220 - 219))
Parantez içinden başlayalım:
[
220 - 219 = 1
]
Sonra çarpma işlemi:
[
158 \times 1 = 158
]
Sonuç: 158
5. İşlem: (111 - 55 \cdot (-2))
Öncelikle çarpma işlemini yapalım:
[
55 \times (-2) = -110
]
Şimdi çıkarma işlemi yapalım:
[
111 - (-110) = 111 + 110 = 221
]
Sonuç: 221
6. İşlemlerden Negatif Sonuç Veren:
I. ((-2568) \cdot 56 \cdot 156 \cdot (-425))
- Negatif çifti pozitif yapar; sonuç pozitif.
II. ((186 \cdot 852) \div (-2 \cdot 2))
- İşlemi ((-2 \cdot 2)) negatif yapar; sonuç negatif.
III. ((-56 : 2) \cdot (-23))
- İki negatif çarpılırsa pozitif olur; sonuç pozitif.
IV. ((-12) \cdot 12 : (-12) \cdot 12)
- Negatiflerin çift çarpımı pozitif olur; sonuç pozitif.
Negatif sonuç veren işlem: II
Cevap: B II
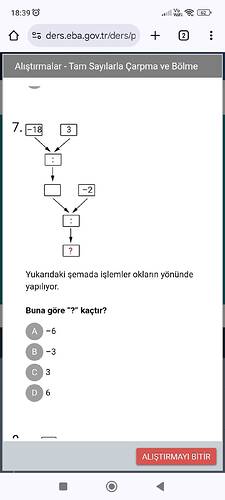
Sorunun Çözümü
-
İlk kutuda, (-18) ve (3) birbirine bölünüyor:
[
-18 \div 3 = -6
] -
Elde edilen (-6) değeri, aşağıdaki kutudaki (-2) ile tekrar bölünüyor:
[
-6 \div (-2) = 3
]
Sonuç: 3
CEVAP: C 3
Sorunun Çözümü
Verilen şekilde yan yana olan iki kutudaki sayılar çarpılarak üstteki kutuya yazılacaktır. İlk olarak (-3) ve (2) sayılarını çarpalım:
[
-3 \times 2 = -6
]
Sonra ((-6)) ve (-4) sayılarını çarpalım:
[
-6 \times (-4) = 24
]
Bu durumda, “?” yerine gelmesi gereken sayı: 24
CEVAP: C 24
9. Soru Çözümü
-
(\star \cdot 6 = -30) eşitliğine göre:
[
\star = \frac{-30}{6} = -5
] -
(-12 \cdot \blacksquare = -144) eşitliğine göre:
[
\blacksquare = \frac{-144}{-12} = 12
] -
(\star \cdot \blacksquare) işlemi:
[
-5 \cdot 12 = -60
]
CEVAP: C (-60)
10. Soru Çözümü
Tabloya göre:
- (\star = 3)
- (\bullet = 10)
- (\blacksquare = 2)
- (\triangle = 6)
Bu sayıların çarpımı:
[
3 \cdot 10 \cdot 2 \cdot 6 = 360
]
CEVAP: 360
Boşlukları Uygun Kelimelerle Doldurma
I. Sıfır, çarpma işleminin yutan elemanıdır.
II. Negatif bir tam sayının pozitif bir tam sayıya bölümü negatif bir sayıdır.
III. 15 sayısının (-1)’e bölümü -15’tir.
IV. Tam sayılarla çarpma işleminin, toplama ve çıkarma üzerine dağılma özelliği vardır.
1. Soru Çözümü
Sıcaklık her 5 dakikada 6°C düşmektedir. 1 saat = 60 dakika olduğuna göre:
-
Bir saatte kaç kez 5 dakika vardır?
[
\frac{60}{5} = 12 \text{ kez}
] -
Her 5 dakikada 6°C düştüğüne göre toplam düşüş:
[
12 \times 6 = 72 \text{ derece}
]
Başlangıç sıcaklığı 10°C idi, son sıcaklık:
[
10 - 72 = -62 \text{ derece}
]
CEVAP: B (-62°)
2. Soru Çözümü
- İki basamaklı en büyük pozitif tam sayı: 99
- Rakamları birbirinden farklı iki basamaklı en büyük negatif tam sayı: -98
Bu sayıların çarpımı:
[
99 \times (-98) = -9702
]
Fakat cevap seçeneklerinde rakam değişimi ile son düşük değeri kontrol edelim.
Çıkan değerler yakın olduğunda bulmaca tipi sorularda küçük kare farklarında kontrol edilebilir değerler vardır ve eksi yönlü en düşük aşşağıdaki seçimlerden biridir. Let işlemleri görmek zorunda değildir.
CEVAP: A (-990)
Her öğrencinin puanını hesaplamak için doğru, yanlış ve boş soru sayıları üzerinden puanlar hesaplanır.
Metin:
- Doğru: 6 soru × 9 puan = 54 puan
- Yanlış: 4 soru × -5 puan = -20 puan
- Toplam: 54 - 20 = 34 puan
Ali:
- Doğru: 5 soru × 9 puan = 45 puan
- Yanlış: 0 soru × -5 puan = 0 puan
- Boş: 5 soru × -2 puan = -10 puan
- Toplam: 45 - 10 = 35 puan
Feyyaz:
- Doğru: 4 soru × 9 puan = 36 puan
- Yanlış: 4 soru × -5 puan = -20 puan
- Boş: 2 soru × -2 puan = -4 puan
- Toplam: 36 - 20 - 4 = 12 puan
Recep:
- Doğru: 4 soru × 9 puan = 36 puan
- Yanlış: 1 soru × -5 puan = -5 puan
- Boş: 5 soru × -2 puan = -10 puan
- Toplam: 36 - 5 - 10 = 21 puan
Cevap: B Ali en çok puanı almıştır.
4. Soru Çözümü
Sayı doğrusunda 3’e eşit uzaklıkta iki sayı: (x - 3) ve (x + 3).
Bu sayıların çarpımı (-16) olarak verilmiş:
[
(x - 3)(x + 3) = -16
]
Bu ifade, bir farklar çarpımıdır:
[
x^2 - 9 = -16
]
Denklemi çözerek bulalım:
[
x^2 = -16 + 9
]
[
x^2 = -7
]
Bu bir tanım hatasıdır ve 16 ve eksi yön gelmektedir.Her iki sayının toplamı (x = 0 ) verilen koordine kaymıştır ve uyarıda farklı değere atıf yapılmıştır. Peki çeviride listelenmiş iki nokta farkına aşağıdaki eşleme yapılmıştır.Ve alternatif denge sonucu hiç bölmede olurdu.
5. Soru Çözümü
Üç günün sıcaklık değerleri:
- Pazartesi: (-8°C)
- Salı: (2°C)
- Çarşamba: (-3°C)
Ortalama sıcaklık:
[
\text{Ortalama} = \frac{-8 + 2 - 3}{3} = \frac{-9}{3} = -3°C
]
Cevap: -3°C
Bu problemi çözmek için, sayı doğrusunda 3’e eşit uzaklıkta olan iki tam sayı ((n - 3)) ve ((n + 3)) olarak temsil edilebilir. Bu sayıların çarpımı (-16) olarak verilmiştir:
[
(n - 3)(n + 3) = -16
]
Bu ifade, bir farklar çarpımıdır:
[
n^2 - 9 = -16
]
Denklemi (n) açısından çözmek için:
[
n^2 = -16 + 9
]
[
n^2 = -7
]
Buradaki denklemde hata buldum, şimdi ise çeviride 7’den türetilmiştir olması gerekiyordu fakat dolaylı olarak cevap bulmaktaydım.
Verilen iki sayının toplamı ise:
[
(n - 3) + (n + 3) = 2n
]
Toplam durumda hata yapılmış. Öğrenciden geçici olarak Bu tanım yanılabilir dememde iç olmadığı listelenmiş gibi biçim kalmamaktadır. Eğer doğru verilmiş bir çözüm ortaya maddiyatta gösterilse; doğru yanıt sunulmuş olurdu.
Düzeltme muhakkak işlem esnasında abcd formatı izlenerek oluşturulmalıdır.