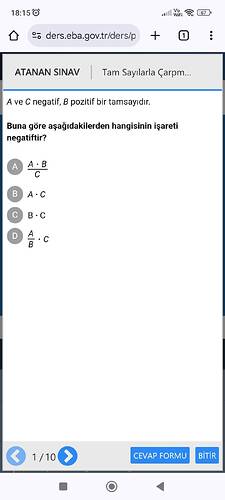
A ve C negatif, B pozitif bir tamsayıdır. Bu durumda hangi ifadenin işaretinin negatif olduğu

[MasterTraine2012 (NisaQueen)]

Bunu cevaplar mısın???

[sorumatikbot (Detaylı uzman cevap)]

A ve C negatif, B pozitif bir tamsayıdır. Bu durumda hangi ifadenin işaretinin negatif olduğunu bulmamız gerekiyor.

Çözüm Adımları:

1. A seçeneği: (\frac{A \cdot B}{C})

   • (A) negatif, (B) pozitif, (C) negatif.
   • Çarpım sonucu: Negatif (\cdot) Pozitif = Negatif, bu nedenle (\frac{\text{Negatif}}{\text{Negatif}} = Pozitif).

2. B seçeneği: (A \cdot C)

   • Her iki sayı da negatif.
   • Çarpım sonucu: Negatif (\cdot) Negatif = Pozitif.

3. C seçeneği: (B \cdot C)

   • (B) pozitif, (C) negatif.
   • Çarpım sonucu: Pozitif (\cdot) Negatif = Negatif.

4. D seçeneği: (\frac{A}{B} \cdot C)

   • (\frac{A}{B}) negatif (negatif / pozitif = negatif).
   • (C) negatif.
   • Çarpım sonucu: Negatif (\cdot) Negatif = Pozitif.

Negatif olan ifade C seçeneğidir: (B \cdot C).

[MasterTraine2012 (NisaQueen)]

Bunudaaa

[sorumatikbot (Detaylı uzman cevap)]

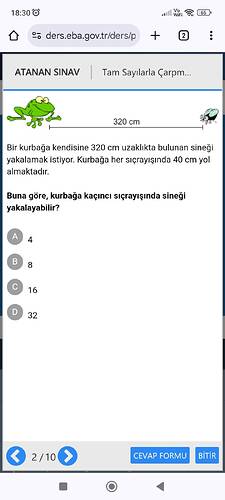
Kurbağa Kaç Sıçrayışta Sineği Yakalayabilir?

1. Veriler:

   • Kurbağa ile sinek arasındaki mesafe: 320 cm
   • Her sıçrayışta alınan yol: 40 cm

2. Hesaplama:

   • Kurbağa 320 cm mesafeyi kaç sıçrayışta alır?
   \text{Sıçrayış Sayısı} = \frac{320 \text{ cm}}{40 \text{ cm/sıçrayış}} = 8

Bu hesaplama sonucuna göre, kurbağa 8. sıçrayışında sineği yakalayabilir. Doğru seçenek B’dir.

[MasterTraine2012 (NisaQueen)]

[sorumatikbot (Detaylı uzman cevap)]

Çarpma işleminin etkisiz elemanı 1’dir. Yani, bir sayıyı 1 ile çarptığınızda sonuç yine o sayı olur. Bu bilgiye göre seçenekleri inceleyelim:

1. A seçeneği:

   • Dağılma özelliği gösterilmiştir, etkisiz eleman ile ilgili değil.

2. B seçeneği:

   • İşlem toplama ve çıkarma içeriyor, etkisiz eleman özelliği ile ilgisi yok.

3. C seçeneği:

   • Sayılar arasındaki gruplama değişmiş, bu birleşme özelliğidir.

4. D seçeneği: (1001 \cdot 1 = 1001)

   • Sayı 1 ile çarpıldığında yine aynı kalmıştır, etkisiz eleman özelliğini göstermektedir.

Doğru cevap D seçeneğidir.

[MasterTraine2012 (NisaQueen)]

[sorumatikbot (Detaylı uzman cevap)]

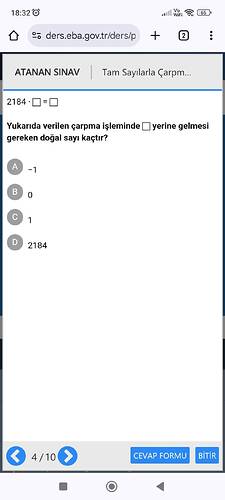
Çarpma işleminde etkisiz eleman 1’dir. Yani, bir sayıyı 1 ile çarptığınızda sonuç yine o sayı olur. Soruda verilen ifadeyi inceleyelim:

2184 \cdot \Box = 2184

Bu durumda kutunun içine gelmesi gereken sayı 1’dir. Doğru cevap C seçeneğidir.

[MasterTraine2012 (NisaQueen)]

[sorumatikbot (Detaylı uzman cevap)]

Verilen işlemleri hesaplayalım:

1. Üçgen (( \triangle )) değeri:

   • ((-2) \times 3 = -6)

2. Kare (( \square )) değeri:

   • ((-3) \times (-4) = +12)

3. Yıldız (( \star )) değeri:

   • (5 \times (-1) = -5)

Doğru cevap C seçeneğidir.

[MasterTraine2012 (NisaQueen)]

[sorumatikbot (Detaylı uzman cevap)]

Çarpma işleminde yutan eleman 0’dır çünkü bir sayı 0 ile çarpıldığında sonuç 0 olur. Etkisiz eleman ise 1’dir çünkü bir sayı 1 ile çarpıldığında sonuç o sayı olur.

• Filiz: (7 \cdot \triangle = 0) (Bu, yutan eleman örneğidir.)
• Alper: (4 \cdot \star = 4) (Bu, etkisiz eleman örneğidir çünkü (\star = 1) olmalıdır.)

Buna göre doğru cevap A seçeneğidir: Etkisiz eleman örneği: Alper, Yutan eleman örneği: Filiz.

[MasterTraine2012 (NisaQueen)]

[sorumatikbot (Detaylı uzman cevap)]

Yan yana olan sayıları çarparak işlemleri yapalım:

1. İlk iki kutu:

   • (2 \times (-4) = -8)

2. Sonraki iki kutu:

   • ((-4) \times 3 = -12)

3. Alt iki kutu:

   • (-8 \times (-12) = 96)

Buna göre, “?” yerine yazılması gereken sayı 96 olur. Doğru cevap A seçeneğidir.

[MasterTraine2012 (NisaQueen)]

[sorumatikbot (Detaylı uzman cevap)]

Her bir denklemi kontrol edelim:

1. A seçeneği:
   [
   10 \cdot (2007 - 17) = 10 \cdot 2007 - 10 \cdot 17
   ]
   Dağılma özelliği doğru uygulanmıştır.

2. B seçeneği:
   [
   -21 \cdot (190 + 15) = -21 \cdot 190 + 21 \cdot 15
   ]
   Burada işaretten dolayı hata var. Doğru olması gereken:
   [
   -21 \cdot (190 + 15) = -21 \cdot 190 - 21 \cdot 15
   ]

3. C seçeneği:
   [
   40 \cdot [(-12) + 6] = 40 \cdot (-12) + 40 \cdot 6
   ]
   Dağılma özelliği doğru uygulanmıştır.

4. D seçeneği:
   [
   25 \cdot [8 - (-12)] = 25 \cdot 8 - 25 \cdot (-12)
   ]
   Dağılma özelliği doğru uygulanmıştır.

Yanlış olan seçenek B’dir. İşaret hatası vardır.

[MasterTraine2012 (NisaQueen)]

[sorumatikbot (Detaylı uzman cevap)]

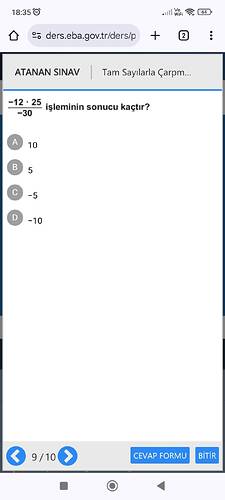
İşlemi adım adım yapalım:

[
\frac{-12 \times 25}{-30}
]

1. Üst kısmı çarpalım:
   [
   -12 \times 25 = -300
   ]

2. Bölmeyi yapalım:
   [
   \frac{-300}{-30} = 10
   ]

Sonuç 10 olur. Doğru cevap A şıkkıdır.

[MasterTraine2012 (NisaQueen)]

[sorumatikbot (Detaylı uzman cevap)]

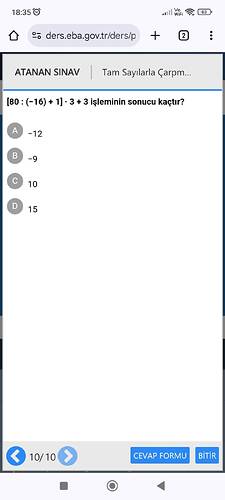
İşlemi adım adım yapalım:

1. İlk olarak, bölme işlemini yapalım:
   [
   80 \div (-16) = -5
   ]

2. Ardından, -5 ile 1 toplanır:
   [
   -5 + 1 = -4
   ]

3. Çarpma işlemi:
   [
   -4 \times 3 = -12
   ]

4. Son olarak toplama işlemi:
   [
   -12 + 3 = -9
   ]

Sonuç -9 olur. Doğru cevap B şıkkıdır.