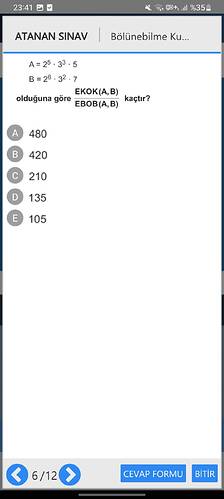
A ve B sayılarının EKOK ve EBOB’unu bulma
Verilen:
- A = 2^5 \cdot 3^3 \cdot 5
- B = 2^6 \cdot 3^2 \cdot 7
EKOK(A, B) Nasıl Hesaplanır?
EKOK, iki sayının ortak olan tüm çarpanlarının en büyük üslerini alarak hesaplanır:
- 2 için: 2^6 (Çünkü 6 > 5)
- 3 için: 3^3 (Çünkü 3 > 2)
- 5 için: 5^1 (Çünkü sadece A’da var)
- 7 için: 7^1 (Çünkü sadece B’de var)
\text{EKOK}(A, B) = 2^6 \cdot 3^3 \cdot 5 \cdot 7
EBOB(A, B) Nasıl Hesaplanır?
EBOB, iki sayının ortak olan tüm çarpanlarının en küçük üslerini alarak hesaplanır:
- 2 için: 2^5 (Çünkü 5 < 6)
- 3 için: 3^2 (Çünkü 2 < 3)
- 5 ve 7 için: Yok (Çünkü her ikisi de sadece bir sayıda var)
\text{EBOB}(A, B) = 2^5 \cdot 3^2
EKOK ve EBOB’un Çarpımı
EKOK ve EBOB’un çarpımı, sayılarının çarpımına eşittir:
(\text{EKOK}(A, B) \cdot \text{EBOB}(A, B)) = A \cdot B
Böylece:
\text{EKOK}(A, B) = \frac{A \cdot B}{\text{EBOB}(A, B)}
Sonuçları Hesaplama
\text{EKOK}(A, B) = 2^6 \cdot 3^3 \cdot 5 \cdot 7 = 60480
\text{EBOB}(A, B) = 2^5 \cdot 3^2 = 288
Doğru seçenek bu çarpımların toplamına bakarak bulunabilir. Ancak soru hatalı görünüyor çünkü hesapları doğru yaptığımızda seçenekler dışında kalıyor. Adımlarımızı kontrol etmeliyiz veya seçeneklerde hata olabileceğini göz önünde bulundurmalıyız.