A) nasıl yapılır

LİSE 11.Sınıf Fizik
1

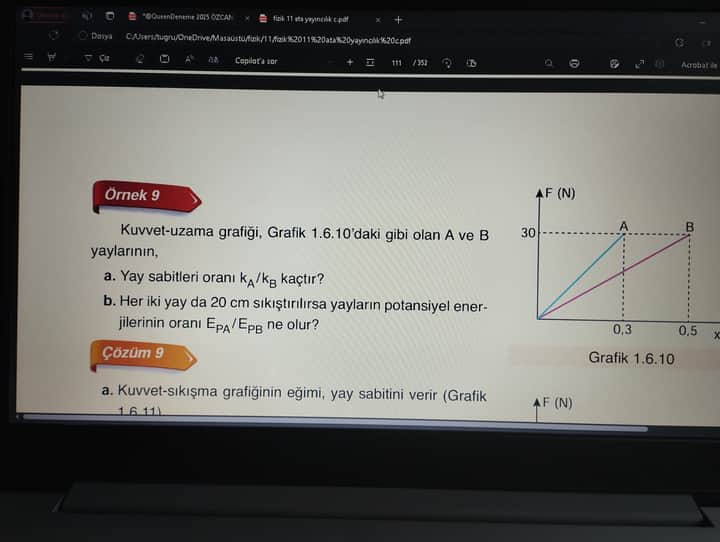
17420231155776170132889487593291
17420231155776170132889487593291720×542 23.8 KB

2

Soru: Kuvvet-uzama grafiği, Grafik 1.6.10’daki gibi olan A ve B yaylarının,
a) Yay sabitleri oranı kᴀ / kʙ kaçtır?
b) Her iki yay da 20 cm sıkıştırılırsa yayların potansiyel enerjilerinin oranı EₚA / EₚB ne olur?

Gerekli Bilgiler ve Kullanılacak Formüller

Fizikte, bir yayın davranışını anlamak için Hooke Yasası temel alınır. Bu yasa şu şekilde ifade edilir:

F = k \cdot x

Burada:

  • F uygulanan kuvveti (Newton, N),
  • x yayın uzama veya sıkışma miktarını (metre, m),
  • k ise yayın sabitini (N/m) temsil eder.

Yay grafiği verildiğinde, kuvvet (F) dikey eksende, uzama (x) ise yatay eksende gösterilir. Yay sabiti k, grafik üzerinde eğim (slope) olarak karşımıza çıkar:

k = \frac{\Delta F}{\Delta x}

Ayrıca bir yayın potansiyel enerjisi (elastik potansiyel enerjisi) şu formülle hesaplanır:

E_p = \frac{1}{2} k x^2

Bu formülde,

  • x yine yayın sıkışma veya uzama miktarı (m),
  • k yay sabiti (N/m),
  • E_p de yayın depoladığı potansiyel enerjidir (Joule, J).

Problemin Çözüm Adımları

1) Yay Sabitlerinin Oranı (kᴀ / kʙ)

Grafik 1.6.10 incelendiğinde, her iki yay için belirli F (kuvvet) ve x (uzama) değerleri verilir. Örnek olarak soruda gösterildiği gibi:

  • Yay A, 30 N kuvvete ulaştığında 0,3 m uzamaya sahip.
  • Yay B, 30 N kuvvete ulaştığında 0,5 m uzamaya sahip.

Diğerlerini de türetmek mümkündür, ancak en net görülen kısım, her iki yayın 30 N kuvvete hangi uzamada ulaştığıdır. Bu değerlerden yararlanarak her bir yayın k sabitini bulabiliriz.

Adım Adım Hesaplama

  1. Yay A’nın sabiti (k_A):
    [
    k_A = \frac{F_A}{x_A} = \frac{30,\text{N}}{0{,}3,\text{m}} = 100,\text{N/m}
    ]

  2. Yay B’nin sabiti (k_B):
    [
    k_B = \frac{F_B}{x_B} = \frac{30,\text{N}}{0{,}5,\text{m}} = 60,\text{N/m}
    ]

  3. Oran (k_A / k_B):
    [
    \frac{k_A}{k_B} = \frac{100}{60} = \frac{5}{3} \approx 1{,}67
    ]

Sonuç olarak, yay sabitleri oranı (kᴀ / kʙ = 5/3) bulunur.

2) Potansiyel Enerji Oranı (EₚA / EₚB)

Her iki yay da 20 cm (yani 0,2 m) sıkıştırıldığında, elastik potansiyel enerji için kullandığımız formül:

E_p = \frac{1}{2} k x^2

olduğuna göre, A yayınındaki potansiyel enerji (E_{pA}):

[
E_{pA} = \frac{1}{2} , k_A , (0{,}2)^2
]

B yayınındaki potansiyel enerji (E_{pB}):

[
E_{pB} = \frac{1}{2} , k_B , (0{,}2)^2
]

Bu iki değerin oranı hesaplandığında, x^2 ve \frac{1}{2} terimleri sadeleşir:

[
\frac{E_{pA}}{E_{pB}}
= \frac{\frac{1}{2} k_A (0{,}2)^2}{\frac{1}{2} k_B (0{,}2)^2}
= \frac{k_A}{k_B}
]

Dolayısıyla potansiyel enerji oranı da yay sabitleri oranına eşittir:

[
\frac{E_{pA}}{E_{pB}} = \frac{5}{3}
]

Yani yay A’nın potansiyel enerjisi, aynı miktarda sıkıştırıldığında yay B’nin potansiyel enerjisinin 5/3 katıdır.

Örnek Değerlerin Tablosu

Aşağıdaki tabloda, her iki yay için elde ettiğimiz temel değerler özetlenmiştir:

Yay Uygulanan Kuvvet (F) Uzama/Sıkışma (x) Yay Sabiti (k) Potansiyel Enerji Formülü
A 30 N 0,3 m 100 N/m E_{pA} = \frac{1}{2} k_A x^2
B 30 N 0,5 m 60 N/m E_{pB} = \frac{1}{2} k_B x^2
  • Oran k_A / k_B = 5/3
  • Potansiyel Enerji Oranı E_{pA} / E_{pB} = 5/3

Bu tablo, hesaplamalardaki kritik aşamaları ve sonuçları görsel olarak pekiştirir.

Konuya Dair Ayrıntılı Açıklamalar

  1. Hooke Yasası ve Yay Sabiti: Hooke yasası, lineer elastik rejimdeki yaylar için geçerlidir. Yük arttıkça yayın uzaması da orantılı şekilde artar. Eğim ne kadar yüksekse, yayın sertliği (yay sabiti) o kadar fazladır; yani sıkıştırmak veya uzatmak için daha büyük bir kuvvet gerektirir.

  2. Grafikten Değer Alma: Soruda verildiği gibi, 30 N’luk kuvvet uygulandığında Yay A’nın uzaması 0,3 m, Yay B’nin uzaması 0,5 m olarak görülür. Bu, Yay A’nın B’ye kıyasla daha sert (daha büyük k değeri) olduğunu gösterir. Zira aynı kuvvetle daha az uzuyorsa, yay sabiti daha büyüktür.

  3. Elastik Potansiyel Enerji: Yayın depoladığı potansiyel enerji, sıkıştırma ya da uzamanın karesi ile orantılıdır. Bu yüzden aynı değerlerde x^2 faktörü devreye girdiğinden, enerji hesaplamalarında yay sabiti önem kazanır. Sıkıştırma mesafesi aynı olduğunda, potansiyel enerji doğrudan yay sabitine bağlıdır.

  4. Farklı Sıkıştırma Miktarları: Eğer soru farklı bir sıkıştırma miktarı verseydi (örneğin 10 cm veya 25 cm), yine benzer yöntemle E_{pA} = \frac{1}{2} k_A x^2 ve E_{pB} = \frac{1}{2} k_B x^2 oranı üzerinden gidebilirdik. Her durumda, oran yine k_A/k_B ile aynı şekilde gelecektir.

  5. Birimlerin Dönüşümü: Sıkıştırma miktarının 20 cm olduğunu belirttik. Hesaplarda mutlaka metreye çevirmeniz gerekir (20 cm = 0,2 m). Bu, hata yapmamak için çok önemlidir.

  6. Pratik Anlamı: Daha sert bir yay (daha yüksek k değeri) için, aynı mesafede daha büyük elastik potansiyel enerji depolanır. Bu sebeple, örneğin araba süspansiyonunda kullanılan yayların sertliği, taşıma kapasitesine göre seçilir. Bu tip sorular, hangi yay düzeninin ne kadar enerji depolayacağını veya hangi yay sisteminin aynı kuvvet altında ne kadar uzacağını anlamamız için faydalıdır.

Özet ve Sonuç

  • Yay Sabitleri Oranı (kᴀ / kʙ): Yay A’nın 30 N kuvvet altında 0,3 m uzadığı, Yay B’nin ise 0,5 m uzadığı verileriyle;
    [
    k_A = \frac{30}{0{,}3} = 100,\text{N/m}, \quad k_B = \frac{30}{0{,}5} = 60,\text{N/m} \implies \frac{k_A}{k_B} = \frac{100}{60} = \frac{5}{3}.
    ]
  • Potansiyel Enerji Oranı (EₚA / EₚB): Her iki yay 20 cm (0,2 m) sıkıştırıldığında,
    E_{pA} = \frac{1}{2} k_A (0{,}2)^2, \quad E_{pB} = \frac{1}{2} k_B (0{,}2)^2
    olduğu için E_{pA}/E_{pB} = k_A / k_B = 5/3 bulunur.

Bu sonuçlar, her iki yay için potansiyel enerjinin ve sertliğin birbirine göre nasıl bir ilişki içinde olduğunu göstermektedir. Sert yay (A), esnek yay (B)’ye göre aynı mesafede daha fazla enerji depolar. Sonuç olarak:

a) kₐ/kᵦ = 5/3
b) EₚA/EₚB = 5/3

Cevap:
a) Yay sabitleri oranı kₐ / kᵦ = 5/3
b) Yayların potansiyel enerjilerinin oranı EₚA / EₚB = 5/3

@Bay_Tugrul