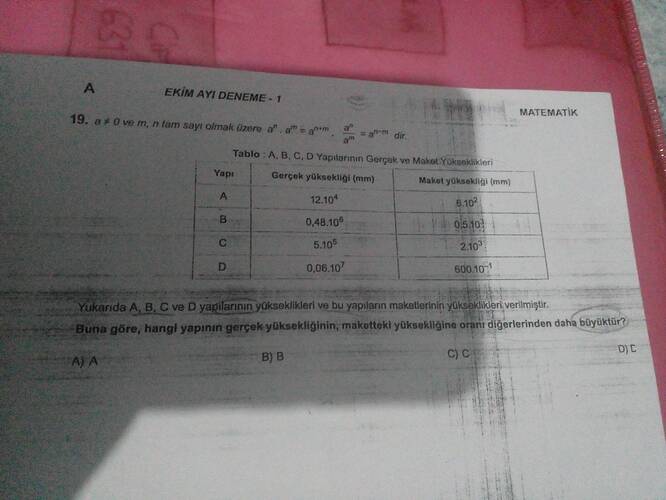
Öncelikle verilen oranları hesaplamamız gerekiyor. Her yapı için gerçek yüksekliğin maket yüksekliğine oranını bulalım:
Yapı A:
Gerçek yükseklik: (12.10^4)
Maket yükseklik: (6.10^2)
Oran:
[
\frac{12 \times 10^4}{6 \times 10^2} = \frac{12}{6} \times 10^{2} = 2 \times 10^2 = 200
]
Yapı B:
Gerçek yükseklik: (0.48 \times 10^5)
Maket yükseklik: (0.5 \times 10^3)
Oran:
[
\frac{0.48 \times 10^5}{0.5 \times 10^3} = \frac{0.48}{0.5} \times 10^{2} = 0.96 \times 10^2 = 96
]
Yapı C:
Gerçek yükseklik: (5.10^5)
Maket yükseklik: (2.10^3)
Oran:
[
\frac{5 \times 10^5}{2 \times 10^3} = \frac{5}{2} \times 10^{2} = 2.5 \times 10^2 = 250
]
Yapı D:
Gerçek yükseklik: (0.06 \times 10^7)
Maket yükseklik: (600 \times 10^{-1})
Oran:
[
\frac{0.06 \times 10^7}{600 \times 10^{-1}} = \frac{0.06}{600} \times 10^{8} = 0.0001 \times 10^8 = 100
]
Bu hesaplara göre oranların büyüklüğü şu şekildedir:
- Yapı A: 200
- Yapı B: 96
- Yapı C: 250
- Yapı D: 100
Sonuç olarak, gerçek yüksekliğin maket yüksekliğine oranı en büyük olan yapı C’dir.
Cevap: C) C