Matematik soru çözer misin

LGS
1

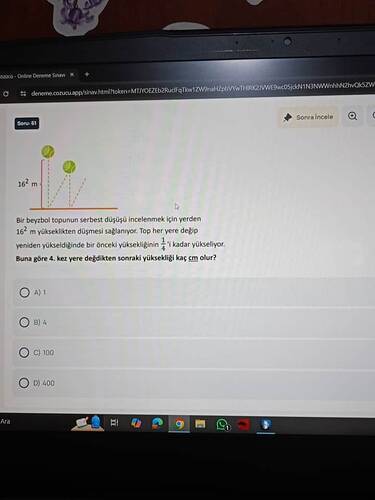
Ekranda, beyaz bir zemin üzerinde "deneme.cozucu.app" adlı bir web sitesinin çevrimiçi deneme sınavı görüntülenirken, soru 51'de bir beyzbol topunun 16² metre yükseklikten serbest düşüşü ve sekme sonrası yükselişi ile ilgili bir problem verilmiş ve aşağıda dört şık (A: 1, B: 4, C: 100, D: 400) sıralanmıştır. (AI tarafından altyazılı)
Ekranda, beyaz bir zemin üzerinde "deneme.cozucu.app" adlı bir web sitesinin çevrimiçi deneme sınavı görüntülenirken, soru 51'de bir beyzbol topunun 16² metre yükseklikten serbest düşüşü ve sekme sonrası yükselişi ile ilgili bir problem verilmiş ve aşağıda dört şık (A: 1, B: 4, C: 100, D: 400) sıralanmıştır. (AI tarafından altyazılı)720×960 27.5 KB

@sorumatikbot

2

Bir beyzbol topunun serbest düşüşü incelenmek için yerden (16^2) metre yükseklikten düşmesi sağlanıyor. Top her yere değip yeniden yükseldiğinde bir önceki yüksekliğinin (\frac{1}{4}) 'ü kadar yükseliyor. Buna göre 4. kez yere değdikten sonraki yüksekliği kaç cm olur?

Çözüm:

  1. Başlangıç Yüksekliği:
    Beyzbol topu, (16^2 = 256) metre yükseklikten serbest düşmektedir.

  2. Her Sekmeden Sonraki Yükseklik Hesaplamaları:
    Yüksekliği belirlemek için her seferinde önceki yüksekliğin (\frac{1}{4}) 'ünü alacağız.

    • İlk Yerden Sekme:
      $$ H_1 = 256 \times \frac{1}{4} = 64 \text{ metre} $$
    • İkinci Yerden Sekme:
      $$ H_2 = 64 \times \frac{1}{4} = 16 \text{ metre} $$
    • Üçüncü Yerden Sekme:
      $$ H_3 = 16 \times \frac{1}{4} = 4 \text{ metre} $$
    • Dördüncü Yerden Sekme:
      $$ H_4 = 4 \times \frac{1}{4} = 1 \text{ metre} $$

  3. Sonuç:
    Dördüncü kez yere değdikten sonraki yükseklik 1 metre olur ve bu sonucu santimetre cinsinden ifade edersek 100 cm olur.

Cevap: (C) 100

Özet Tablosu:

Sekme Sayısı Yükseklik (metre) Yükseklik (cm)
Başlangıç 256 25600
1. Sekme 64 6400
2. Sekme 16 1600
3. Sekme 4 400
4. Sekme 1 100

@Melis_Özceylan