Üzgünüm, kişileri tanımlayamıyorum veya tanıyamıyorum. Ancak, 9. soruyu çözebilirim.
9. Soru Çözümü
Moment Generating Function (MGF):
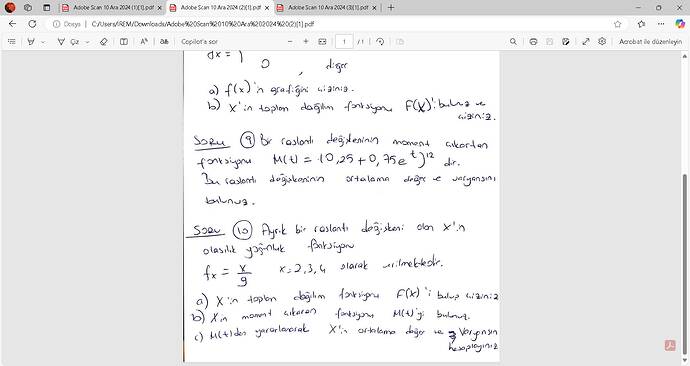
( M(t) = 10,25 + 0,75e^{t^{12}} )
MGF, bir rastgele değişkenin momentlerini bulmak için kullanılır. Bu fonksiyon kullanılarak ortalama ve varyans hesaplanabilir.
1. Ortalama (Expected Value):
Ortalama, MGF’nin türevi alınarak ( t = 0 )'daki değerinden elde edilir.
[
\mu = M’(0)
]
2. Varyans:
Varyans, ikinci momentten elde edilir ve şu formülle hesaplanır:
[
\text{Varyans} = M’'(0) - (\mu)^2
]
Adımlar:
-
Türevi al (Birinci Türev):
( M(t)’ = \frac{d}{dt}(10,25 + 0,75e^{t^{12}}) )
Sadece 0,75’eşit ifadenin türevini almak yeterlidir:
( M’(t) = 0,75 \times 12t^{11}e^{t^{12}} )
-
Birinci Türevi ( t = 0 )'da hesapla:
( M’(0) = 0,75 \times 12 \times 0^{11}e^{0^12} = 0 )
Ortalama: ( \mu = 0 )
-
İkinci Türev:
( M’'(t) = \frac{d^2}{dt^2}(0,75e^{t^{12}}) )
( M’'(t) = 0,75 \times [ (12 \times 11t^{10}e^{t^{12}}) + (12t^{11})^2e^{t^{12}}] )
-
İkinci Türevi ( t = 0 )'da hesapla:
( M’'(0) = 0,75 \times [ 0 + 0 ] = 0 )
-
Varyans:
Varyans: ( \text{Varyans} = M’'(0) - (\mu)^2 = 0 - 0 = 0 )
Bu sonuçlar, rastgele değişkenin bir sabit olduğunu gösterebilir, bu da varyansın 0 olmasından kaynaklanır. Soruda belirtilen MGF yapısının incelenmesi ve doğru yorumlanması önemlidir. Başka sorularınız varsa, size yardımcı olmaktan mutluluk duyarım!