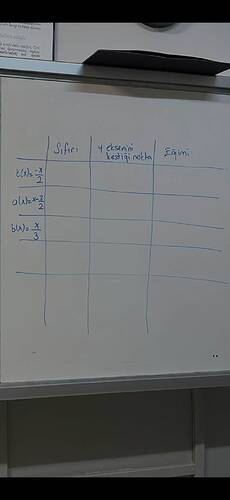
Görüntüdeki tablo, üç farklı fonksiyonun sıfırlarını, y eksenini kestiği noktaları ve eğimlerini bulmamızı istiyor. Bu fonksiyonlar:
- ( k(x) = -\frac{x}{2} )
- ( o(x) = x - \frac{3}{2} )
- ( b(x) = \frac{x}{3} )
Bu fonksiyonları inceleyelim:
Fonksiyonların Sıfırları
Bir fonksiyonun sıfırını bulmak için, fonksiyonu sıfıra eşitleyip ( x ) değerini bulmalıyız.
( k(x) = -\frac{x}{2} )
[ -\frac{x}{2} = 0 ]
Çözüm: [ x = 0 ]
( o(x) = x - \frac{3}{2} )
[ x - \frac{3}{2} = 0 ]
Çözüm: [ x = \frac{3}{2} ]
( b(x) = \frac{x}{3} )
[ \frac{x}{3} = 0 ]
Çözüm: [ x = 0 ]
Y Eksenini Kestiği Nokta
Y eksenini kesen nokta için ( x = 0 ) yerine koyarız.
( k(x) = -\frac{x}{2} )
[ k(0) = -\frac{0}{2} = 0 ]
( o(x) = x - \frac{3}{2} )
[ o(0) = 0 - \frac{3}{2} = -\frac{3}{2} ]
( b(x) = \frac{x}{3} )
[ b(0) = \frac{0}{3} = 0 ]
Fonksiyonların Eğimi
Verilen fonksiyonlar doğrusal olduğu için eğimleri, fonksiyonların başındaki sabit katsayılardır.
( k(x) = -\frac{x}{2} )
Eğimi: (-\frac{1}{2})
( o(x) = x - \frac{3}{2} )
Eğimi: (1)
( b(x) = \frac{x}{3} )
Eğimi: (\frac{1}{3})
Tablo Olacak Şekilde
| Fonksiyon | Sıfırı | Y Eksenini Kestiği Nokta | Eğimi |
|---|---|---|---|
| ( k(x) ) | 0 | 0 | (-\frac{1}{2}) |
| ( o(x) ) | (\frac{3}{2}) | (-\frac{3}{2}) | 1 |
| ( b(x) ) | 0 | 0 | (\frac{1}{3}) |
Bu bilgiler, her bir fonksiyonun grafiksel özelliklerini hızlıca anlamamıza yardımcı olur.