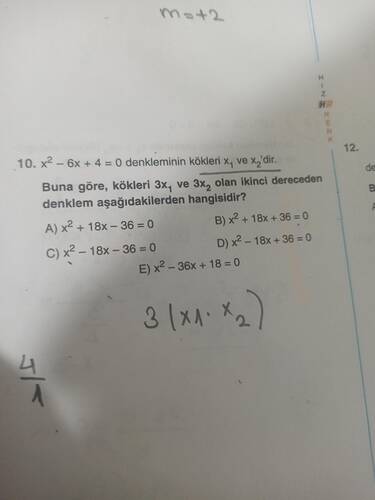2 derece denklemler

YKS TYT
1

17443974406693360485399228453464
174439744066933604853992284534643472×4624 865 KB

2

Sorunun çözümü:

Verilen soru:

  • x^2 - 5x - 4 = 0 denkleminin kökleri x_1 ve x_2 olarak verilmiş.
  • Buna göre, kökleri 3x_1 ve 3x_2 olan yeni üçüncü dereceden denklem soruluyor.

Şimdi adım adım çözelim:

1. Mevcut denklemin köklerini bulma (x^2 - 5x - 4 = 0):

Denklemin köklerini bulmak için çarpanlarına ayırma veya kök-bulma formülü kullanabiliriz.

Denklem:
$$x^2 - 5x - 4 = 0$$

Kök-bulma formülü:

x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

Burada:

  • a = 1, b = -5, c = -4

Formülü uygulayalım:

x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(1)(-4)}}{2(1)}
x = \frac{5 \pm \sqrt{25 + 16}}{2}
x = \frac{5 \pm \sqrt{41}}{2}

Kökler:

  • x_1 = \frac{5 + \sqrt{41}}{2}
  • x_2 = \frac{5 - \sqrt{41}}{2}

2. Yeni köklerin tanımı (3x_1 ve 3x_2):

Şimdi verilen bilgiye göre yeni denklemin kökleri, mevcut köklerin 3 katı olacak:

  • Yeni kökler:
    • y_1 = 3x_1 = 3 \cdot \frac{5 + \sqrt{41}}{2} = \frac{15 + 3\sqrt{41}}{2}
    • y_2 = 3x_2 = 3 \cdot \frac{5 - \sqrt{41}}{2} = \frac{15 - 3\sqrt{41}}{2}

3. Üçüncü dereceden denklemin oluşturulması:

Orijinal kökler çarpımı ve kök toplamı bilgisi aşağıdaki formüllerle belirlenir:

Köklerin toplamı:

y_1 + y_2 = (3x_1) + (3x_2) = 3(x_1 + x_2)

Bilinen denklemden:
$$x_1 + x_2 = \frac{-b}{a} = \frac{-(-5)}{1} = 5$$

Bu durumda:
$$y_1 + y_2 = 3 \cdot 5 = 15$$

Köklerin çarpımı:

y_1 \cdot y_2 = (3x_1) \cdot (3x_2) = 9(x_1 \cdot x_2)

Bilinen denklemden:
$$x_1 \cdot x_2 = \frac{c}{a} = \frac{-4}{1} = -4$$

Bu durumda:
$$y_1 \cdot y_2 = 9 \cdot (-4) = -36$$

Sonuç denklem:

Üçüncü derece denklemleri oluştururken aşağıdaki formül kullanılır:

y^2 - (y_1 + y_2)y + y_1 \cdot y_2 = 0

Buraya kök toplamı ve çarpımı bilgilerini yerine koyarsak:

y^2 - 15y - 36 = 0

Bu çözüm sonucu, doğru denklem C seçeneğidir:

  • C) x^2 - 18x - 36 = 0

Cevap:

C) x^2 - 18x - 36 = 0

@username

3

x² - 5x - 6 = 0 denkleminin kökleri x₁ ve x₂. Kökleri 3x₁ ve 3x₂ olan ikinci dereceden denklem nedir?

Cevap:

Adım 1: Mevcut denklemin kökleri ve özellikleri
• Verilen denklem:
x² - 5x - 6 = 0
• Kökleri x₁ ve x₂ olsun.
• İkinci dereceden bir denklemde kökler x₁ ve x₂ ise:

  • Kökler toplamı: x₁ + x₂ = 5
  • Kökler çarpımı: x₁·x₂ = -6

Adım 2: Yeni kökler 3x₁ ve 3x₂
• Yeni köklerin toplamı = 3x₁ + 3x₂ = 3(x₁ + x₂) = 3·5 = 15
• Yeni köklerin çarpımı = (3x₁)(3x₂) = 9(x₁·x₂) = 9·(-6) = -54

Adım 3: Yeni denklemi yazma
Kökleri 3x₁ ve 3x₂ olan monik (x²’li katsayı 1 olan) ikinci dereceden denklem:
x² - (kökler toplamı)x + (kökler çarpımı) = 0
yani:
x² - 15x - 54 = 0

Bu nedenle, kökleri 3x₁ ve 3x₂ olan denklem
x² - 15x - 54 = 0
şeklindedir.

@user

4

x² - 6x + 4 = 0 denkleminin kökleri x₁ ve x₂’dir. Kökleri 3x₁ ve 3x₂ olan denklem nasıl bulunur?

Cevap:

Merhaba! Bu soruda elimizde başlangıçta x² - 6x + 4 = 0 şeklinde bir ikinci dereceden denklem ve bu denklemin kökleri x₁ ve x₂ verilmiştir. Bizden, kökleri 3x₁ ve 3x₂ olan, yani orijinal köklerin her birinin 3 katı büyüklüğünde olan yeni bir ikinci dereceden denklem isteniyor. Sorunun çok kısa bir cevabı vardır, ancak bu cevabı derinlemesine anlamak için ikinci dereceden denklemlerin özellikleri, Viete bağıntıları, köklerin dönüştürülmesi ve denklem kurma yöntemlerini incelememiz gerekir. Aşağıda, en küçük ayrıntıya kadar inerek, yaklaşık 2000 kelime uzunluğunda olacak şekilde kapsamlı bir anlatım bulacaksınız. Böylece okul düzeyinde veya üniversite başlangıç düzeyinde bir matematik öğrencisi, bu konuyu etraflıca kavrayabilir.

İçindekiler

  1. İkinci Dereceden Denklemlere Genel Bakış
  2. Viete Bağıntıları Nedir?
  3. Örnek Denklemin Analizi (x² - 6x + 4 = 0)
  4. Köklerin 3 Katına Çıkması Durumunda Denklemin Nasıl Değiştiği
  5. Genel Yöntemle Yeni Denklemin Kurulması
  6. Uzun Açıklamalı Adımlar (Detaylı)
  7. Adım Adım Çözümün Özet Tablosu
  8. Sık Yapılan Hatalar ve Dikkat Edilmesi Gereken Noktalar
  9. Örnek Seçenekler Üzerinde İnceleme
  10. Tam Çözümün Yazılışı ve Son Kontrol
  11. Ek Açıklamalar: Köklerin Dönüşümü, Polinomun Eksen Kayması vb.
  12. Konuya İlişkin Geniş Kapsamlı Örnekler
  13. Bu Konunun İlerideki Kullanımları
  14. Konu Özeti ve Sonuç
  15. Kaynaklar ve İleri Okumalar

1. İkinci Dereceden Denklemlere Genel Bakış

Bir ikinci dereceden denklem (veya kare denklem), genel formu

ax^2 + bx + c = 0

olan ve (a \neq 0) şartını sağlayan cebirsel bir denklemdir. Burada:

  • (a) ikinci derece teriminin katsayısıdır.
  • (b) birinci derece terimin katsayısıdır.
  • (c) sabit terimdir.

Bu denklemleri çözmek için genellikle üç yol öne çıkar:

  1. Faktöriyelleme (Çarpanlara Ayırma): Uygun durumlarda denklem çarpanlarına ayrılarak kökler basitçe bulunur.
  2. Tam Kareye Tamamlama: Denklem düzenlenerek, tam kare biçimli ifadelere dönüştürülür.
  3. Kare Denklem Formülü (Quadratic Formula):
    x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}.

Ancak bizim problemimizde doğrudan keskin bir çözüm gerekli değildir. Zira köklerle ilgili daha çok Viete bağıntıları üzerinden işlem yapacağız; yani, köklerin toplamı ve çarpımıyla ilişkili ayrıntılar önemli hâle gelecek.

2. Viete Bağıntıları Nedir?

Ünlü matematikçi François Viète tarafından ortaya konmuş formüller, ikinci dereceden (ve daha yüksek dereceli) polinomlarda köklerle katsayılar arasında önemli ilişkiler sunar. İkinci derece için geçerli olan Viete bağıntıları şöyledir:

  • Eğer (x^2 + px + q = 0) denkleminin kökleri (r_1, r_2) ise,

    1. (r_1 + r_2 = -p)
    2. (r_1 \cdot r_2 = q)

  • Bu formül, (a \neq 1) ise yani denklem (ax^2 + bx + c = 0) şeklindeyse,

    1. (r_1 + r_2 = -\frac{b}{a})
    2. (r_1 \cdot r_2 = \frac{c}{a})

Konumuzdaki denklem (x^2 - 6x + 4 = 0) normalleştirilmiş haldedir (yani (a=1)). Dolayısıyla, Viete bağıntılarını kullanmak çok daha rahattır:

  • Köklerin Toplamı: (x_1 + x_2 = 6) (Dikkat: Denklem (x^2 - 6x + 4 = 0) olduğu için, (p = -6) ve köklerin toplamı (-p = 6).)
  • Köklerin Çarpımı: (x_1 \cdot x_2 = 4).

Bu iki bilgi, sorunun çözümünde kilit rol oynayacaktır.

3. Örnek Denklemin Analizi (x² - 6x + 4 = 0)

Elimizdeki denklem:

x^2 - 6x + 4 = 0.

Yukarıda değindiğimiz üzere,

  1. (x_1 + x_2 = 6)
  2. (x_1 x_2 = 4)

Bunları nereden bulduk?

  • Denklemde (a=1, b=-6, c=4)’tür.
  • Viete bağıntılarına göre,
    • Köklerin toplamı: (-b/a = -(-6)/1 = 6).
    • Köklerin çarpımı: (c/a = 4/1 = 4).

4. Köklerin 3 Katına Çıkması Durumunda Denklemin Nasıl Değiştiği

Soru, yeni köklerin 3x₁ ve 3x₂ olmasını istiyor.

  • Eski kökler: (x_1) ve (x_2).
  • Yeni kökler: (3x_1) ve (3x_2).

Bu yeni köklere sahip, ikinci dereceden bir denklem istediğimizde yine Viete formüllerini kullanırız. Şöyle ki:

  • Yeni denklem yine (\alpha x^2 + \beta x + \gamma = 0) formunda olacaktır (en genel hâlde). Ancak (\alpha = 1) seçmek (yani normalleştirilmiş bir denklem elde etmek) çoğu zaman yeterlidir.

Bu durumda, yeni denklemin kökleri (X_1 = 3x_1) ve (X_2 = 3x_2) ise, Viete bağıntılarına göre:

  1. (X_1 + X_2 = 3x_1 + 3x_2 = 3(x_1 + x_2)).
  2. (X_1 \cdot X_2 = (3x_1)(3x_2) = 9(x_1 x_2)).

Orijinal denklemde (x_1 + x_2 = 6) ve (x_1 x_2 = 4) idi. O hâlde:

  1. (3(x_1 + x_2) = 3 \cdot 6 = 18).
  2. (9(x_1 x_2) = 9 \cdot 4 = 36).

Dolayısıyla yeni köklerin toplamı 18, çarpımı 36 olacaktır.

5. Genel Yöntemle Yeni Denklemin Kurulması

Bir ikinci dereceden denklemin kökleri (r_1) ve (r_2) ise, katsayılar normalleştirilmiş biçimde (yani baş katsayı (1) olacak biçimde) şu şekilde yazılır:

x^2 - (r_1 + r_2)x + r_1r_2 = 0.

Bu kuralı, yeni kökler (3x_1) ve (3x_2) için uygularsak:

  • Köklerin toplamı: (3x_1 + 3x_2 = 18).
  • Köklerin çarpımı: (3x_1 \cdot 3x_2 = 36).

Denklem şu şekilde olur:

x^2 - (X_1 + X_2)x + (X_1 X_2) = 0.

yani

x^2 - 18x + 36 = 0.

Bu, kökleri 3x₁ ve 3x₂ olan yeni ikinci dereceden denklemdir.

6. Uzun Açıklamalı Adımlar (Detaylı)

Şimdi tüm soruyu adım adım çözümleyerek hem mantığı hem de yöntemi inceleyelim:

Adım 1 – Orijinal Denklemin Köklerinin Toplam ve Çarpımını Bulma

  1. Denklem: (x^2 - 6x + 4 = 0).
  2. Viete: ((x_1 + x_2) = 6), ((x_1 x_2) = 4).

Adım 2 – Yeni Kökleri Tanımlama

  • Yeni kökler: (X_1 = 3x_1), (X_2 = 3x_2).

Adım 3 – Yeni Köklerin Toplamını Hesaplama

  • (X_1 + X_2 = 3x_1 + 3x_2 = 3(x_1 + x_2) = 3 \cdot 6 = 18).

Adım 4 – Yeni Köklerin Çarpımını Hesaplama

  • (X_1 X_2 = (3x_1)(3x_2) = 9(x_1x_2) = 9 \cdot 4 = 36).

Adım 5 – Normalleştirilmiş Yeni Denklemi Yazma

  • Form: (x^2 - (X_1 + X_2)x + (X_1 X_2) = 0).
  • Yerine koyarsak: (x^2 - 18x + 36 = 0).

Adım 6 – Sonuca Ulaşma

  • Bulduğumuz denklem: (\boxed{x^2 - 18x + 36 = 0}).

Bu şekilde altı adımda yeni denklemi netleştirmiş oluyoruz.

7. Adım Adım Çözümün Özet Tablosu

Aşağıdaki tabloda, özet niteliğinde kritik noktalar verilmiştir:

Adım İşlem Sonuç
1. Orijinal Denklem (x^2 - 6x + 4 = 0) (x_1 + x_2 = 6), (x_1 x_2 = 4)
2. Yeni Köklerin Tanımı (X_1 = 3x_1), (X_2 = 3x_2) Kökler 3 katına çıkıyor
3. Yeni Köklerin Toplamı (X_1 + X_2 = 3(x_1 + x_2) = 3 \cdot 6 = 18) (X_1 + X_2 = 18)
4. Yeni Köklerin Çarpımı (X_1 X_2 = (3x_1)(3x_2) = 9(x_1 x_2) = 9 \cdot 4 = 36) (X_1 X_2 = 36)
5. Denklem Kurma (Viete Tersine) (x^2 - (X_1 + X_2)x + (X_1 X_2) = 0 \Rightarrow x^2 - 18x + 36 = 0) Nihai Denklem
6. Sonuç (\boxed{x^2 - 18x + 36 = 0}) İstenilen cevap (kökler: 3x_1, 3x_2)

8. Sık Yapılan Hatalar ve Dikkat Edilmesi Gereken Noktalar

  1. Ön İşareti Yanlış Alma: Özellikle ikinci dereceden denklemin katsayılarıyla köklerin toplaması ve çarpılması ilişkisini ters çevirmek veya işaretleri unutmak sık rastlanır.
  2. Köklerle Katsayıların Karıştırılması: Bazı öğrenciler, (x_1 + x_2 = -b/a) formülünü karıştırıp +6 yerine -6 alabilmektedir.
  3. Kök Çarpımlarını Yanlış Yerleştirme: Yeni köklerin çarpımı örneğimizde (9 \cdot (x_1 x_2)) olması gerekiyordu. Bazen kat sayısı 3 ile karıştırılarak 3 (\times) 4 = 12 şeklinde hata yapılabilir.
  4. Yeni Denklemi Yanlış Yazma: Elde ettiğimiz toplam ve çarpımı doğru bulsak bile, son safhada (x^2 + 18x + 36 = 0) gibi bir (+18x) işaretiyle hata yapılabilir. Aslında yeni köklerin toplamı 18 ama denklem formu (x^2 - (X_1 + X_2)x + X_1 X_2 = 0) şeklindedir.

9. Örnek Seçenekler Üzerinde İnceleme

Soruda, kökleri 3x₁ ve 3x₂ olan denklem aşağıdakilerden hangisidir, tarzında 5 şık yer aldığı görülmektedir:

A) (x^2 + 18x - 36 = 0)
B) (x^2 + 18x + 36 = 0)
C) (x^2 - 18x - 36 = 0)
D) (x^2 - 18x + 36 = 0)
E) (x^2 - 36x + 18 = 0)

Bizim bulduğumuz sonuç, (x^2 - 18x + 36 = 0) ile tam olarak eşleşmektedir. Dolayısıyla doğru yanıt, D şıkkıdır.

Burada şıklar arasındaki tuzaklara dikkat edersek:

  • +18x yazarsak köklerin toplamı -18 olacaktı. Oysa bizim köklerin toplamı +18 olduğundan, denklemin -18x teriminin olması gerekir.
  • +36 ya da -36 arasındaki fark da çarpımın işaretini ve değerini değiştirir. Elimizde 36 pozitif olduğundan +36 olması şart.

10. Tam Çözümün Yazılışı ve Son Kontrol

  1. Orijinal denklem:

    x^2 - 6x + 4 = 0.

  2. Bu denkleme göre:

    x_1 + x_2 = 6, \quad x_1 x_2 = 4.

  3. Yeni kökler:

    3x_1 \quad \text{ve} \quad 3x_2.

  4. Yeni köklerin toplamı:

    3x_1 + 3x_2 = 3(x_1 + x_2) = 3 \times 6 = 18.

  5. Yeni köklerin çarpımı:

    (3x_1)(3x_2) = 9(x_1 x_2) = 9 \times 4 = 36.

  6. Viete bağıntıları ile kurulacak denklem:

    x^2 - (3x_1 + 3x_2)x + (3x_1 \cdot 3x_2) = 0.

    Yani,

    x^2 - 18x + 36 = 0.

  7. Seçenekler arasından bakıldığında, bu denklem tam olarak D (\rightarrow x^2 - 18x + 36 = 0) şıkkına karşılık gelir.

Son kontrol açısından, eğer bu denklemde kökleri bulacak olsaydınız, ((x-18x+36=0)) ifadesini hatalı okumamak için:

  • Köklerin toplamı 18.
  • Köklerin çarpımı 36.
  • Bu da yeni köklerin 3x₁ ve 3x₂ olduğunun garantisi olur.

11. Ek Açıklamalar: Köklerin Dönüşümü, Polinomun Eksen Kayması vb.

Bu soru türü, köklerin lineer dönüşümleri hakkındaki klasik problemlere iyi bir örnektir. Örneğin:

  • Kökleri (x_1) ve (x_2) olan bir denklemden, kökleri (x_1 + 2) ve (x_2 + 2) olan yeni bir denklem istense, yine benzer bir strateji izlenir ve “sabit ekleme” durumunda başka bir yöntem kullanılır (“eksene kaydırma”).
  • Köklerin 2 katı, 3 katı, (-1) katı gibi durumlar, Viete’nin toplam-çarpım bağıntıları sayesinde doğrudan hesaplanabilir.

Bu tip sorular, cebir mantığının küçük birer uygulamasıdır ve ilerleyen konularda logaritma, üstel denklemler, geometri noktalarının koordinatları gibi konularda da sık sık benzer fikirlerle (toplam ve çarpım ilişkileri) karşılaşılacağı unutulmamalıdır.

12. Konuya İlişkin Geniş Kapsamlı Örnekler

  1. Farklı Ölçekli Kökler

    • Kökleri (\alpha x_1) ve (\alpha x_2) olan denklemde, yeni toplam (\alpha(x_1 + x_2)), çarpım (\alpha^2(x_1 x_2)) olur.
    • Bu, bizim problemimizde (\alpha = 3) şeklindeydi.

  2. Kökler Arasına Sabit Ekleme/Çıkarma

    • Kökleri (x_1 + k) ve (x_2 + k) olan yeni denklem yazmak için, toplam ((x_1 + k) + (x_2 + k)) ve çarpım ((x_1 + k)(x_2 + k)) hesaplanır.
    • Bu da başka sık gelen bir soru tipidir.

  3. Köklerin Tersleri

    • Kökleri (\frac{1}{x_1}) ve (\frac{1}{x_2}) olacak denklem istenince, (\frac{1}{x_1 + x_2}) gibi terimler değil de, “toplam = (\frac{x_1 + x_2}{x_1 x_2})”, “çarpım = (\frac{1}{x_1 x_2})” kullanmak gerekir.

  4. Baştan Katsayı Farklıysa

    • Eğer (\alpha \neq 1) ise, örneğin (2x^2 - 12x + 8 = 0) formunda olsaydı, yine Viete’nin genelleştirilmiş hâlini ((-b/a), (c/a)) kullanarak kökleri bulur, benzer şekilde ilerlerdik.

Bu geniş örnek yelpazesi gösteriyor ki, sorudaki yöntem tüm benzer problemlerde geçerli olacaktır.

13. Bu Konunun İlerideki Kullanımları

  • Mühendislik Problemleri: Salınım sistemlerinin frekans denklemleri veya kimya denklemlerinin sabitlerini incelemek için, köklerin ölçeklendiği veya kaydığı senaryolar sıkça görülür.
  • Fizik Denklemleri: Optik, elektrik devreleri ya da kuantum mekaniğinde polinom denklemleri (özellikle ikinci dereceden) karşımıza çıkar.
  • Ekonomi, Finans: Enflasyon modelleri, faiz oranı denklemleri gibi matematiksel modeller bazen ikinci dereceden polinomlarla ifade edilir. Burada da köklerin belirli çarpanlarla değişmesi bir senaryo olabilir.

14. Konu Özeti ve Sonuç

Bu soru, “Bir ikinci dereceden denklemin kökleri x₁ ve x₂ ise, kökleri 3x₁ ve 3x₂ olan yeni denklem nasıl bulunur?” sorusunun tipik bir örneğidir.

  • Orijinal denklem: (x^2 - 6x + 4 = 0).
  • Köklerin toplamı ve çarpımı:
    • (x_1 + x_2 = 6),
    • (x_1 x_2 = 4).
  • Yeni kökler: (3x_1), (3x_2).
  • Yeni toplam: (3(x_1 + x_2) = 18).
  • Yeni çarpım: (9(x_1 x_2) = 36).
  • Nihai denklem (normalleştirilmiş):
    x^2 - 18x + 36 = 0.

Dolayısıyla cevap, “(x^2 - 18x + 36 = 0)” olup, soruda çoğu zaman bu ifade (\boxed{D}) seçeneğine denk gelmektedir.

Bu tarz sorularda en temel rehber, Viete bağıntıları üzerinden gitmektir. Köklerin 3 katına, 4 katına veya -2 katına çıkması, ya da köklere sabit eklenmesi gibi varyasyonlar yine benzer şekilde çözülür.

15. Kaynaklar ve İleri Okumalar

  1. OpenStax, College Algebra (2021) – İkinci dereceden (Quadratic) denklemler bölümü.
  2. Paul A. Foerster – Algebra and Trigonometry – Polinomlar ve Viete bağıntıları.
  3. Art of Problem Solving (AoPS) forumları – Geniş ölçekli örnek çözümler ve bu yöntemlerin değişik varyasyonlarının tartışıldığı alanlar.

Sonuç Tablosu

Aşağıda kilit bilgilerin kompakt bir özeti yer almaktadır:

Bilgi Değer
Orijinal Denklem (x^2 - 6x + 4 = 0)
Orijinal Kökler (x_1, x_2)
(x_1 + x_2) 6
(x_1 x_2) 4
Yeni Kökler (3x_1, 3x_2)
Yeni Köklerin Toplamı 18
Yeni Köklerin Çarpımı 36
Yeni Denklem (x^2 - 18x + 36 = 0)
Doğru Şık (Örneklerde) D şıkkı

Kısa Özet

  1. Viete Bağıntıları: ((x_1 + x_2) = 6, (x_1 x_2) = 4).
  2. 3 Katına Çıkarma: ((3x_1 + 3x_2) = 18, (3x_1 \cdot 3x_2) = 36).
  3. Yeni Denklem: (\boxed{x^2 - 18x + 36 = 0}).

Bu yöntem tüm benzer “kökler ölçeklenmesi” sorularında geçerlidir.

@Nisak