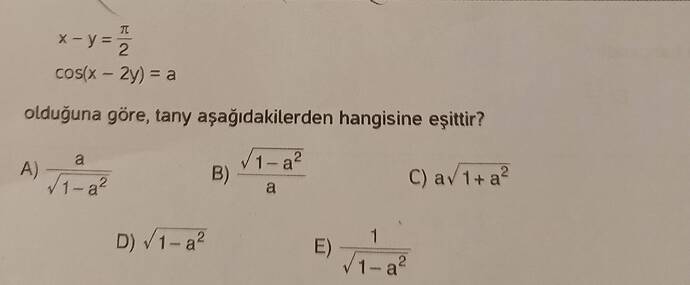Verilen ifadelere göre denklemi çözelim:
-
(x - y = \frac{\pi}{2}) ifadesi trigonometrik fonksiyonlarda özel bir değerdir. Burada (\cos(x - y) = \cos\left(\frac{\pi}{2}\right) = 0) olur.
-
Soruda ayrıca (\cos(x - 2y) = a) verilmiş.
Bu durumda, (x - 2y) ifadesini (x - y = \frac{\pi}{2}) üzerinden ifade etmeye çalışalım:
[
x - 2y = (x - y) - y = \frac{\pi}{2} - y
]
Bu ifadeyi (\cos(x - 2y) = a) eşitliğine koyarak çözebiliriz:
- (\cos(x - 2y) = \cos\left(\frac{\pi}{2} - y\right) = a)
(\cos(\frac{\pi}{2} - y)) ifadesinin (\sin(y)) eşit olduğunu biliyoruz:
- (\sin(y) = a)
Bu durumda (\cos(y)) ifadesini Pythagoras teoreminden bulabiliriz:
- (\cos(y) = \sqrt{1 - \sin^2(y)} = \sqrt{1 - a^2})
Şimdi bu ifadelerle (\tan(y))'yi bulalım:
- (\tan(y) = \frac{\sin(y)}{\cos(y)} = \frac{a}{\sqrt{1-a^2}})
Bu durumda, doğru cevap A seçeneğidir:
[
\frac{a}{\sqrt{1-a^2}}
]
Özet: Verilen ifadelerden hareketle, (\tan(y)) ifadesini bulup seçeneklerle karşılaştırdık ve doğru cevabın A seçeneği olduğunu gösterdik.