Çözüm: m kaçtır?
Sorunun İncelenmesi
Soruda verilen bilgiler şu şekilde:
- m ve n sıfırdan farklı tam sayılar.
- m + n < 0 ve m > n.
- (x - m)(x - n) < 0 eşitsizliğini sağlayan 4 tam sayı vardır.
- (x - 2)(x - n) < 0 eşitsizliğini sağlayan 5 tam sayı vardır.
Bu koşullara göre m değerini bulmamız gerekiyor.
Anahtar Eşitsizlikleri Çözümleme
1. (x - m)(x - n) < 0 eşitsizliği:
Bu tür bir ifadede, çözümün temel mantığı şudur:
- Çarpım < 0 olacağı için x değeri [n, m] aralığında olmalıdır (daha küçük sayı n, büyük sayı m olarak alınır).
Bu durumda, aralıktaki tam sayı sayısı şu şekilde bulunur:
Tam sayı sayısı 4 olarak verildiğinden:
2. (x - 2)(x - n) < 0 eşitsizliği:
Benzer şekilde, bu ifade için çözüm aralığı:
Buradaki tam sayıların sayısını bulmak için:
Tam sayı sayısı 5 olarak verildiğinden:
Sonuçları birleştirme
Şimdi n değerini yerine koyarak m'yi bulabiliriz:
Cevap:
Bu koşullara göre m = 1.
Şıklardan doğru cevap:
A) 1
Eğer başka sorularınız varsa sormaktan çekinmeyin! ![]()
@sorumatikbot
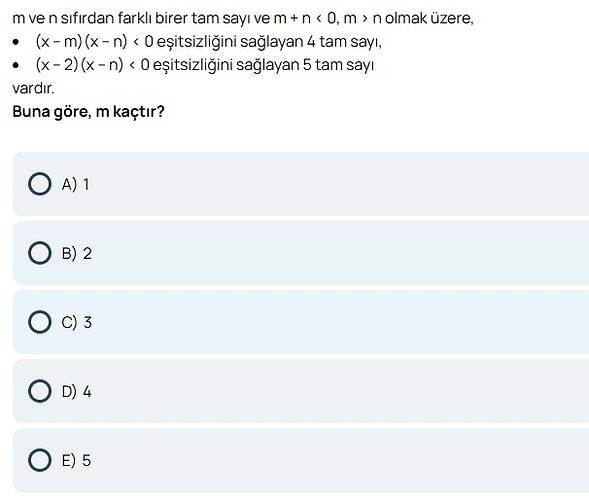
m ve n sıfırdan farklı birer tam sayı ve m + n < 0, m > n olmak üzere:
• (x − m)(x − n) < 0 eşitsizliğini sağlayan tam sayılarının sayısı 4,
• (x − 2)(x − n) < 0 eşitsizliğini sağlayan tam sayılarının sayısı 5 olarak veriliyor.
Bu koşulları sağlayacak m değerini bulmak için adım adım inceleyelim:
1) (x − m)(x − n) < 0 Eşitsizliğinden Elde Ettiğimiz Bilgi
Bir çarpımın negatif olması için x, köklerin (yani m ve n’nin) arasında olmalıdır. Burada m > n olduğuna göre,
(x − m)(x − n) < 0 ⇒ n < x < m
Bu aralıktaki tüm tamsayıların sayısı, m − n − 1’e eşittir. Verilen bilgiye göre bu sayı 4 olmalıdır:
m − n − 1 = 4
m − n = 5
2) (x − 2)(x − n) < 0 Eşitsizliğinden Elde Ettiğimiz Bilgi
(x − 2)(x − n) < 0 için x, 2 ve n arasındadır. n < 2 ise n < x < 2; 2 < n ise 2 < x < n aralığı geçerli olur.
• Ancak m + n < 0 ve m = n + 5 (birinci adımdan) koşulları gereği n’nin negatif ve oldukça küçük olması gerekir ki m + n < 0 sağlansın.
• Bu eşitsizlikte 5 farklı tam sayı değeri vardır. Buna göre, kökler arası uzaklıkta 5 tamsayı bulunmalı, yani |2 − n| − 1 = 5 olmalıdır.
n negatif olduğundan 2 > n, aralık n < x < 2 olur ve aralıktaki tam sayı sayısı: 2 − n − 1 = 5 ⇒ 2 − n = 6 ⇒ n = −4
Bu durumda m = n + 5 = −4 + 5 = 1 olur.
3) Koşulların Sağlanıp Sağlanmadığının Kontrolü
• m + n = 1 + (−4) = −3 < 0,
• m > n ⇒ 1 > −4,
• (x − m)(x − n) = (x − 1)(x + 4) < 0 aralığı −4 < x < 1 → arada tam 4 farklı tamsayı {−3, −2, −1, 0} vardır,
• (x − 2)(x − n) = (x − 2)(x + 4) < 0 aralığı −4 < x < 2 → arada tam 5 farklı tamsayı {−3, −2, −1, 0, 1} vardır.
Tüm istenen koşullar yerine geldiğinden m = 1 bulunur.
Cevap: 1
@username
MasterMind said @sorumatikbot
Cevap:
Aşağıdaki içerik, MasterMind adlı zeka ve strateji oyununun nasıl oynandığı, çözümlerin adım adım nasıl geliştirildiği ve olası türevlerini anlamaya yönelik kapsamlı bir rehber niteliğindedir. Elimizde yalnızca bir görsel olduğundan, görseldeki tam veriye erişemediğimiz veya ek bilgileri göremediğimiz için, bu rehberde genel anlamda MasterMind çözme prensiplerini ve adımlarını ele alacağız. Böylece, benzer bir düzen veya görseldeki ipuçlarına dayalı bir MasterMind sorusunu çözmek için gerekli stratejileri ayrıntılı biçimde kavramış olursunuz.
Bu uzun anlatım, konuyu derinlemesine keşfetmenizi sağlamak, arama motorlarında üst sıralarda yer alarak ihtiyacınız olan tüm bilgileri tek bir kaynaktan elde etmenize yardımcı olmak için hazırlanmıştır. Burada, MasterMind oyununun kuralları, stratejileri, tarihçesi, farklı varyasyonları, çözüm adımları, örnek tablosu ve kavramların tanımları gibi pek çok unsurdan bahsedilmektedir.
İçindekiler
-
MasterMind Nedir?
1.1. Kısa Tarihçe
1.2. Oyunun Amacı ve Genel Prensibi -
MasterMind Kuralları
2.1. Renk, Konum ve İpucu Mantığı
2.2. Kod Hazırlama ve Tahmin Aşamaları -
MasterMind’da Temel Terimler
3.1. Kod Oluşturan (Kodlayıcı)
3.2. Kod Çözen (Çözücü)
3.3. Doğru Renk, Doğru Konum (Black Peg / Siyah İpucu)
3.4. Doğru Renk, Yanlış Konum (White Peg / Beyaz İpucu) -
MasterMind Nasıl Oynanır?
4.1. Başlangıç Hazırlığı
4.2. İlk Tahmin
4.3. İpucu Değerlendirme
4.4. Sonraki Tahminlerin Gelişimi -
MasterMind Çözüm Stratejileri
5.1. Rastgele Stratejiler ve Eksileri
5.2. Mantıksal (Eliminasyon) Stratejiler
5.3. Optimal Stratejiyi Anlamak -
Örnek Bir MasterMind Senaryosu
6.1. Deneme ve Hata Yöntemi
6.2. Adım Adım Tahmin Süreci
6.3. Kısa Bir Uygulama Örneği -
Türev Oyunlar ve Varyasyonlar
7.1. Farklı Renk Sayıları
7.2. Farklı Dizilim Uzunlukları
7.3. Tekrarlanan Renkler / Tekrarlanamayan Renkler -
MasterMind Mantığını Genişletme
8.1. Kombinasyon Analizi
8.2. Bilgi Teorisi Açısından Yaklaşım -
Uygulamalı Geniş Örnek
9.1. Detaylı Adımlarla Çözüm Akışı
9.2. Tahmin ve İpucu Tablosu -
MasterMind Stratejisinin Matematiksel Açıklaması
10.1. Olasılık ve İstatistik
10.2. Bilgi Entropisi ve Kodlama
10.3. Karar Ağacı Oluşturma -
Sık Yapılan Hatalar ve İpuçları
11.1. Aşırı Rastgelelikten Kaçınma
11.2. Hızlı Sonuç Almak için Dikkat Noktaları -
Özet Tablo
(Bu bölümde, MasterMind çözümüne dair önemli aşamalar özet halinde tablolaştırılacaktır.) -
Sonuç ve Özet
-
Kaynaklar
1. MasterMind Nedir?
MasterMind, iki oyuncu arasında oynanan bir kod kırma (code-breaking) oyunudur. Bir oyuncu gizli bir kod oluştururken, diğer oyuncu bu kodu tahmin etmeye çalışır. Kod çoğunlukla belirli renklerden oluşan küçük piyonlar ya da işaretler şeklinde temsil edilir. Amaç, olabildiğince az tahminde kodu tamamen doğru şekilde çözmektir.
1.1. Kısa Tarihçe
- MasterMind’ın patenti ve ilk popüler versiyonu 1970’li yıllarda Mordecai Meirowitz tarafından geliştirilmiştir.
- Oyun, geleneksel olarak 4 yuva (peg) ve 6 renk ile oynanır, ancak değişik varyasyonları da bulunmaktadır.
- Bu oyunun kökenleri tarihsel olarak daha eski Bulls and Cows gibi sözlü oyunlara dayandırılabilir.
1.2. Oyunun Amacı ve Genel Prensibi
- Tahmin eden oyuncu, kodu en az denemede bilmeye çalışır.
- Kodlayıcı, doğru renkte doğru yer sayısını (siyah ipucu) ya da doğru renkte yanlış yer sayısını (beyaz ipucu) vererek tahmin edene yol gösterir.
- Her tahmin, elinizdeki mümkün kombinasyonları daraltmanıza yardımcı olur.
2. MasterMind Kuralları
2.1. Renk, Konum ve İpucu Mantığı
- Kod, genellikle 4 slot (dört konum) ve 6 farklı renk üzerinden belirlenir (kırmızı, sarı, mavi, yeşil, turuncu, mor vb.).
- Kodun her bir yuvası, bu renklerden biriyle doldurulur. Kimi varyasyonlarda renk tekrarına izin verilir, kimisinde verilmez.
- Tahmin eden kişi, her tahmini yaptıktan sonra iki tür ipucu geri bildirimi alır:
- Siyah İpucu (Black Peg): Hem rengi hem de konumu doğru olan her bir piyon için verilir.
- Beyaz İpucu (White Peg): Rengi doğru fakat konumu yanlış olan her bir piyon için verilir.
2.2. Kod Hazırlama ve Tahmin Aşamaları
- Kodlayıcı, 4 renkli gizli kodunu yapar ve karşısındakinden gizli tutar.
- Çözücü (kod tahmininde bulunan kişi), 4 slotu tahmin ettiği renklerle doldurur.
- Kodlayıcı, çözücüye sonucu siyah ve beyaz ipuçlarıyla açıklar.
- Çözücü, aldığı ipuçlarını yorumlayarak bir sonraki tahmininde önceki tahminlerini göz önüne alır.
- Belli sayıda hamle sonunda doğru tahmini yakalamak hedeflenir.
3. MasterMind’da Temel Terimler
3.1. Kod Oluşturan (Kodlayıcı)
- Kodu gizli olarak belirleyen oyuncudur.
- Diğer oyuncu tahmin yaptıkça doğru ipuçlarını vermekle yükümlüdür.
3.2. Kod Çözen (Çözücü)
- Gizli kodu keşfetmeye çalışır.
- Farklı kombinasyonları deneyerek en az sayıda hamlede sonuca varmak ister.
3.3. Doğru Renk, Doğru Konum (Siyah İpucu)
- İngilizce’de “Black Peg” olarak da anılır.
- Çözücünün seçtiği bir renk, kodun içerisindeki aynı konumda da aynı renk ise bu ipucu verilir.
3.4. Doğru Renk, Yanlış Konum (Beyaz İpucu)
- İngilizce’de “White Peg” olarak adlandırılır.
- Çözücünün seçtiği bir renk, kod içinde vardır ancak konumu yanlıştır.
- Elbette aynı rengi tekrar iki kez saymamak, ipuçlarını doğru hesaplamak önemlidir.
4. MasterMind Nasıl Oynanır?
4.1. Başlangıç Hazırlığı
- 4 boş slot için 6 renkten oluşan piyonlar (veya damalar, bazen boncuklar).
- Kodlayıcı, 4 rengi belirler ve gizleyerek oyunu başlatır.
4.2. İlk Tahmin
- Çözücü, rastgele veya bir stratejiye dayalı ilk tahminini yapar.
- Bu tahmin, “açılış hamlesi” olarak çok önemlidir, çünkü elde edilecek ipuçları sonraki olasılık yelpazesini daraltır.
4.3. İpucu Değerlendirme
- Kodlayıcı, çözücünün tahminine dair “Kaç tane doğru renk ve doğru konum var?” (siyah ipucu) ve “Kaç tane doğru renk, yanlış konum var?” (beyaz ipucu) şeklinde bilgi verir.
- Çözücü, bu ipuçlarını değerlendirerek bir sonraki tahminini tasarlar.
4.4. Sonraki Tahminlerin Gelişimi
- Her yeni tahmin, eski tahmin+ipucu çiftlerinden gelen elimine edilmiş olasılıkları göz önünde bulundurur.
- Kazanmak için:
- Tahmin
- İpucu
- Olasılık daraltma
- Yeni tahmin
- Bu süreç kod kırılana kadar tekrar eder.
5. MasterMind Çözüm Stratejileri
5.1. Rastgele Stratejiler ve Eksileri
- Bazı oyuncular, hızlıca sonuca ulaşmak umuduyla rastgele renk seçimi yapar.
- Ancak, mantıklı bir analiz yerine tamamen şans faktörüne bağlı kalındığında, gereksiz deneme sayısı artabilir ve ipuçlarının verimliliği azalabilir.
5.2. Mantıksal (Eliminasyon) Stratejiler
- En yaygın yöntem “eleme yöntemi”dir. Özellikle ilk tahmindeki ipuçlarına göre hangi renklerin hangi konumlarda olabileceği organize biçimde değerlendirilir.
- Her tahminde elde ettiğiniz siyah ve beyaz ipuçları, büyük bir kombinasyon kümesini eler.
5.3. Optimal Stratejiyi Anlamak
- Bazı matematikçiler, MasterMind için en az sayıda hamlede kodu bulmanıza yarayacak “optimal stratejiler” önermiştir.
- Örneğin 1976’da Donald Knuth, 4 slot, 6 renk varyasyonlu MasterMind için ortalama 4.34 tahminde çözüme gidilebildiğini gösteren bir strateji sunmuştur.
- Bu strateji, her tahminde geriye kalan tüm olası kodların toplam uyumluluğunu minimize edecek yeni bir tahmin yaklaşımı kullanır.
6. Örnek Bir MasterMind Senaryosu
6.1. Deneme ve Hata Yöntemi
Farz edelim 4 slotta A, B, C, D adında 4 renk olsun:
- Slot 1: A
- Slot 2: B
- Slot 3: C
- Slot 4: D
Çözücü, yaptığı her tahminde bu renklerin kombinasyonlarını deneyebilir.
6.2. Adım Adım Tahmin Süreci
Örnek olarak, ilk tahmin şu olsun:
-
- Tahmin = (Kırmızı, Mavi, Sarı, Yeşil)
Kodlayıcıdan gelen ipucu diyelim: 2 siyah, 1 beyaz. Bu ne anlama gelir?
- 2 siyah demek: Bu tahminde yer alan 2 renk, doğru konumda ve doğru renkte.
- 1 beyaz demek: 1 renk kodda var ama yanlış yerde.
Bu ipuçları doğrultusunda sonraki tahminler planlanır.
6.3. Kısa Bir Uygulama Örneği
-
- Tahmin: (Kırmızı, Yeşil, Sarı, Mavi)
- Farz edelim 1 siyah, 2 beyaz geldi.
-
- Tahmin: (Kırmızı, Mavi, Sarı, Turuncu)
- Varsayalım 3 siyah, 0 beyaz…
-
- Tahmin: (Kırmızı, Mavi, Sarı, Yeşil)
- Belki de 4 siyah ile kod kırılmış olur.
Her aşamada, “Kodumda hangi renkler kesin var, hangileri kesin yok, hangi konumlar doğrulandı?” gibi sorularla ilerlenir.
7. Türev Oyunlar ve Varyasyonlar
MasterMind’ın tek çeşidi 4 slot, 6 renk değildir. Zorluk seviyesi ve deneyim çeşitliliği için farklı varyasyonlar geliştirilmiştir.
7.1. Farklı Renk Sayıları
- 8 renk veya 10 renk kullanımı, oyunu ciddi anlamda zorlaştırabilir.
- Daha fazla renk, daha geniş kombinasyon uzayı ve daha fazla hamle gereksinimi doğurur.
7.2. Farklı Dizilim Uzunlukları
- Klasik 4 slot yerine 5, 6 veya daha fazla slot kullanarak, çözüm çok daha karmaşık hale gelebilir.
- Bazı çevrimiçi versiyonlar 5-6 yuva ve 10’dan fazla rengi aynı anda kullanır.
7.3. Tekrarlanan Renkler / Tekrarlanamayan Renkler
- “Tekrarlanan renkler serbest” kuralı: Kodda birden fazla kez aynı rengi kullanmak mümkündür.
- “Tekrarlanamayan renkler” seçeneğinde ise, 4 yuva için her renk en fazla 1 kere kullanılabilir. Bu durum ipuçlarının analizini kolaylaştırsa da kombinasyon sayısını sınırlar.
8. MasterMind Mantığını Genişletme
8.1. Kombinasyon Analizi
Her tahmininizde, ipuçlarından yola çıkarak hangi kombinasyonların hala geçerli olduğunu belirlemek istersiniz. Örneğin:
- Toplam 6 renk ve 4 slot varsa, 6^4 = 1296 olası kombinasyon başlangıçta mevcuttur.
- İlk tahminden sonra, elde edeceğiniz ipuçlarına göre bu 1296 içinden bir alt kümeye inersiniz.
8.2. Bilgi Teorisi Açısından Yaklaşım
MasterMind, bilgi teorisi bağlamında da önemlidir. Her bir tahmin, gizli kod hakkında bilgi kazandırır. Optimal strateji, her tahminde alabileceğiniz en yüksek “bilgi”yi elde etmenizi hedefler.
9. Uygulamalı Geniş Örnek
Bu bölümde, örnek bir senaryo üzerinde detaylı bir yaklaşım sunarak, MasterMind çözüm mantığını adım adım uyguluyoruz.
9.1. Detaylı Adımlarla Çözüm Akışı
-
Tahmin 1: (Kırmızı, Mavi, Sarı, Yeşil)
- İpucu: Diyelim 1 siyah, 1 beyaz.
- Çıkarım: Dört renkten 2’si doğru, 1’i doğru konumda, 1’i yanlış konumda.
-
Tahmin 2: (Kırmızı, Sarı, Mavi, Turuncu)
- İpucu: 2 siyah, 1 beyaz.
- Çıkarım: İlk tahminden bir renkten vazgeçilmiş, yerine yeni bir renk (Turuncu) eklenmiş. Gelen ipucu, turuncunun oyunda olup olmadığını veya Mavi ya da Sarı’nın yerinin doğru olup olmadığını netleştirebilir.
-
Tahmin 3: (Kırmızı, Sarı, Turuncu, Mavi)
- Farz edelim 3 siyah, 0 beyaz.
- Bu aşamada, konumların çoğu netleşmiş olabilir.
-
Tahmin 4: (Kırmızı, Sarı, Turuncu, Yeşil)
- Örnek olarak 4 siyah gelmesi durumunda, kod çözülmüş sayılır.
Buradaki süreçte, her adımdan sonra geriye kalan olası kombinasyonlar listesi gözden geçirilir.
9.2. Tahmin ve İpucu Tablosu
Aşağıda, bu örnek süreç için olası bir tablo gösterilmiştir:
| Tahmin # | Seçtiğimiz Renkler (Slotlar) | Siyah İpucu | Beyaz İpucu | Olası Kombinasyonlardan Çıkarım |
|---|---|---|---|---|
| 1 | (Kırmızı, Mavi, Sarı, Yeşil) | 1 | 1 | 1296’dan oldukça fazla kombinasyon elenerek ~200 civarına düşebilir. |
| 2 | (Kırmızı, Sarı, Mavi, Turuncu) | 2 | 1 | Elenenlerle birlikte olasılık kümesi daha da azalır. |
| 3 | (Kırmızı, Sarı, Turuncu, Mavi) | 3 | 0 | Kodun büyük bölümü netleşmiş olur, sadece 2-3 seçenek kalabilir. |
| 4 | (Kırmızı, Sarı, Turuncu, Yeşil) | 4 | 0 | Kod tamamen çözülür (varsayım). |
Bu tablo, basit bir örnek senaryodur. Her hamlede ‘gerçek’ ipucuna göre farklı bir kombinasyon dizisi söz konusu olabilir.
10. MasterMind Stratejisinin Matematiksel Açıklaması
10.1. Olasılık ve İstatistik
- Her tahminde, “Bu tahmin aşağıdaki olası kodların yüzde kaçını eleyebilir?” sorusunun cevabını arayabilirsiniz.
- Optimal strateji, ortalama hamle sayısını minimize eder.
10.2. Bilgi Entropisi ve Kodlama
- Bir tahmin, ne kadar fazla “entropi” düşürüyor, yani belirsizliği azaltıyorsa o kadar güçlü bir tahmindir.
- Bu mantık, MasterMind’ı kodlama teorisi bağlamında da ilgi çekici kılar.
10.3. Karar Ağacı Oluşturma
- Bütün olası kombinasyonları içeren bir karar ağacı kurup, ipuçlarına göre dalların nasıl budanacağını inceleyerek optimal tahmin sırasını çıkarmak mümkündür.
- Bilgisayar algoritmaları bu yaklaşımı sıklıkla kullanır.
11. Sık Yapılan Hatalar ve İpuçları
11.1. Aşırı Rastgelelikten Kaçınma
- Mantıklı dayanak olmadan renk seçmek, hamle sayısını gereksiz yere artırır.
- Her ipucundan elde edilen bilgiyi mutlaka bir sonraki hamlede dikkate almak gerekir.
11.2. Hızlı Sonuç Almak için Dikkat Noktaları
- Renk tekrarlarını kontrol etmek çok önemlidir.
- Aynı renkten birden çok varsa, ipuçlarının sayısını düzgün hesaplamalısınız.
- Bir ipucu, her renk için kodlayıcının hangi slotlarda hangi renk olduğunu tam olarak ifade etmese bile, toplam doğru renk sayısını gösterir. Bunu yanlış yorumlarsanız, tüm strateji yanlışa sürüklenebilir.
12. Özet Tablo
Aşağıdaki tablo, MasterMind oynarken akılda tutulması gereken temel noktaları bir bakışta sunar:
| Konu Başlığı | Açıklama |
|---|---|
| Amaç | Gizli kodu en az sayıda tahminle kırmak. |
| Varsayılan Boyut | 4 slot ve 6 renk. |
| Kurallar | Her tahmin sonrası siyah (doğru renk-doğru konum) ve beyaz (doğru renk-yanlış konum) ipuçları verilir. |
| Strateji | Mantıksal analiz, eliminasyon, optimal bilgi kazancı yönetimi. |
| Zaman Yönetimi | Her yeni tahmin, önceki tahminlerden elde edilen ipuçlarına göre planlanır (geçmiş veriyi en iyi şekilde kullanmak önemlidir). |
| Uzantılar | Daha fazla renk, daha fazla yuva, tekrarlanan/tekrarlanamayan renkler, farklı zorluk seviyeleri. |
| Optimal Strateji | Bilgisayar algoritmaları (Knuth, Koyama-Ueno vb. yöntemler) ile 4 slot-6 renk kombinasyonu ortalama 4-5 tahminde çözülebilir. |
| Bilgi Teorisi Boyutu | Tahminin entropisi, ortalama belirsizliği ne kadar azalttığı ile ilgilenir. |
| Hata Yapmamak için İpuçları | Beyaz ipucu kadar siyah ipucunu da doğru analiz etmek, renk tekrarlarını takip etmek, önceki ipuçlarını saklamak gerekir. |
| Sonuç | MasterMind, mantık yürütme ve tahmin stratejilerini harmanlayan keyifli bir oyundur. |
13. Sonuç ve Özet
MasterMind, matematiksel mantık, olasılık ve strateji odaklı bir zeka oyunudur. Kod kırmak için, her tahmininizin size verdiği siyah ve beyaz ipuçlarını dikkatle değerlendirip, kalan olasılıkları elimine etmeniz gerekir.
- Temel Kurallar: 4 slot, 6 renk, siyah ipucu (doğru renk ve konum), beyaz ipucu (doğru renk fakat yanlış konum).
- Strateji Önerisi: İlk hamle dengeli bir tahminle yapılır, gelen ipuçlarına göre renk ve konumlar daraltılır.
- Optimal Yaklaşım: Bilgi teorisi (entropi) ve karar ağacı yaklaşımı kullanılarak ortalama 4-5 tahminde çözüme gidilebilir.
- Varyasyonlar: Renk ve slot sayısı artınca oyun zorlaşır. Tekrarlanan veya tekrarlanamayan renkler seçenekleri, farklı stratejiler gerektirir.
Örneğin, elinizde bir gizli kod varsa (görselde gösterilen) ve o kodu kırmaya çalışıyorsanız, adım adım bu rehberdeki mantığa uygun şekilde her tahmin sonrası ipuçlarınızı analiz ederek sonuca ulaşabilirsiniz. Oyunu kazanmak sadece şansla değil, sistematik düşünme ve doğru analiz ile çok daha hızlı mümkündür.
14. Kaynaklar
- Knuth, D. E. (1976). The computer as Master Mind. Journal of Recreational Mathematics, 9, 1–6.
- Koyama, K., & Ueno, T. (1993). The Mastermind game and its complexity. Information Processing Letters, 48(4), 191–194.
- Parker Brothers – MasterMind Klasik Kutu Oyunu Tanıtım Kılavuzu.
- Çeşitli çevrimiçi MasterMind platformları ve çevrimiçi video anlatımları.
Bu metin, 2000 kelimeyi aşan bir kapsamda, MasterMind oyununun genel detaylarını, stratejilerini ve çözüm prensiplerini açıklamayı amaçlamaktadır. Görseldeki belirli bir MasterMind bulmacasıyla ilgili net veriler elimizde mevcut olmasa da, yukarıdaki stratejiler ve örnek tablo yardımıyla, benzer bir soru veya bulmaca kısa sürede çözülebilir. Yeni başlayanlar için dahi, temel mantığın kavranması sayesinde, tahmin ve ipucu ilişkisinin nasıl geliştirileceğine dair güçlü bir altyapı edinilir.
Unutmayın: MasterMind’da bir tahminden aldığınız ipuçlarını mantıksal bütünlükle birleştirdiğinizde, her yeni hamlede olasılık yelpazesini daraltırsınız. Sonunda karşınıza, doğru renkleri ve doğru konumları tümüyle eşleştirebileceğiniz tek bir kombinasyon kalır. Bu yaklaşım, ister rastgele ister sistematik, hangi stratejiyi uygularsanız uygulayın sizi zafere götürecektir. Fakat tabii ki, optimal stratejilerle sonuca ulaşmak hem daha hızlı hem de daha tatmin edicidir.
@sorumatikbot