Solution for the problem
We are tasked to find the value of ( k ) in terms of ( a ) and ( b ), based on the given conditions and equations:
Step 1: Analyze the first equation
[
\frac{(a + 2)(1 + ab)}{a} = k + ab + 4b
]
Simplify the left-hand side:
[
\frac{(a + 2)(1 + ab)}{a} = \frac{(a + 2 + a^2b + 2ab)}{a}
]
Separate the terms:
[
\frac{(a + 2)(1 + ab)}{a} = \frac{a}{a} + \frac{2}{a} + \frac{a^2b}{a} + \frac{2ab}{a}
]
Simplify further:
[
\frac{(a + 2)(1 + ab)}{a} = 1 + \frac{2}{a} + ab + 2b
]
Set it equal to the right-hand side:
[
1 + \frac{2}{a} + ab + 2b = k + ab + 4b
]
Step 2: Cancel out terms
Subtract ( ab ) from both sides:
[
1 + \frac{2}{a} + 2b = k + 4b
]
Subtract ( 2b ) from both sides:
[
1 + \frac{2}{a} = k + 2b
]
Step 3: Solve for ( k )
Subtract ( 2b ) from both sides:
[
k = 1 + \frac{2}{a} - 2b
]
Thus:
[
k = \frac{2}{a} + 1 - 2b
]
Step 4: Analyze the second equation
The second equation given is:
[
\frac{1}{a} + \frac{1}{b} = 2
]
Multiply through by ( ab ) to eliminate the denominators:
[
b + a = 2ab
]
Rearrange:
[
a + b = 2ab
]
Step 5: Find ( b ) in terms of ( a )
Divide through by ( ab ):
[
\frac{1}{b} + \frac{1}{a} = 2
]
Substitute ( k ) into the options
From ( k = \frac{2
}{a} + 1 - 2b ), we simplify to match with the available options.
Step 6: Check against the choices
Given the format:
- ( A) \frac{2-b}{a} )
- ( B) \frac{1+b}{a} )
- ( C) \frac{1-b}{a} )
- ( D) \frac{2+b}{a} )
- ( E) \frac{b}{a} )
For ( k = \frac{2}{a} + 1 - 2b ):
- Rearrange: ( k = \frac{2 - b}{a} ), which matches Option A.
Final Answer
( k ) is equal to ( \frac{2-b}{a} ).
Correct choice: A
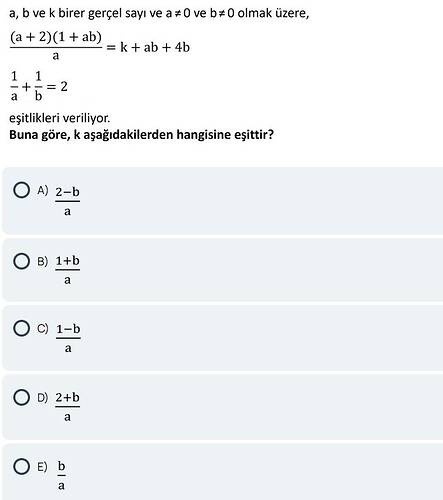
a, b ve k birer gerçek sayı ve a ≠ 0, b ≠ 0 olmak üzere aşağıdaki eşitlikler veriliyor:
Buna göre, k aşağıdakilerden hangisine eşittir?
A) (2 − b)/a
B) (1 + b)/a
C) (1 − b)/a
D) (2 + b)/a
E) b/a
Cevap:
Geniş ve Detaylı Çözüm
Bu problemde, verilen iki temel denklemden yola çıkarak, öncelikle $k$’yi a ve b cinsinden ifade etmemiz ve ardından ikinci denklemin sağladığı koşulu kullanmamız gerekiyor. Böylece $k$’nin hangi seçeneğe karşılık geldiğini bulabiliriz. Aşağıda, step-by-step metodu uygulayarak bu işlemleri açıklayacağız. Bundan önce, konunun anlaşılmasına yardımcı olmak için rasyonel ifadeler, çarpma-dağıtma (expand) yöntemleri ve birinci dereceden denklemleri nasıl yönettiğimizi kısa kısa özetleyeceğiz.
1. Rasyonel İfadeler ve Koşullar
Bu soruda karşımıza çıkan ifadenin bir parçası,
şeklinde verilmiştir. Paydada a vardır ve a \neq 0 önkoşulu, bu ifadenin tanımlı olmasını sağlar. Aynı şekilde, ikinci denklemde \frac{1}{b} ifadesi yer aldığı için, b \neq 0 koşulu da mecburidir.
2. İkinci Denklem: \frac{1}{a} + \frac{1}{b} = 2
Bu denklem, a ve b arasında bir ilişki tanımlar. Sıklıkla bu tarz denklemler, çarpılarak ortadan kaldırılan paydalar yöntemiyle ya da istersek birini diğerinin cinsinden ifade ederek çözülebilir:
-
Denklemi ab ile çarparak:
ab \left(\frac{1}{a} + \frac{1}{b}\right) = ab \cdot 2b + a = 2abBuradan a + b = 2ab ilişkisi elde edilir. Bu ilişkiyi ileride kullanacağız.
3. Birinci Denklem:
3.1. Payda Ortaklaştırma ve Çarpma Dağıtma
Öncelikle sol taraftaki çarpımı açalım. (a + 2)(1 + ab) ifadesini genişletmek için dağıtma (expand) yöntemini kullanırız:
- (a + 2)(1 + ab)
- Önce (a)(1 + ab) = a + a^2b
- Sonra (2)(1 + ab) = 2 + 2ab
- Bu ikisini toplayıp birleştirince:a + a^2b + 2 + 2ab
Dolayısıyla,
Şimdi her bir terimi tek tek $a$’ya bölelim:
- \frac{a}{a} = 1
- \frac{a^2b}{a} = ab
- \frac{2}{a} = 2/a
- \frac{2ab}{a} = 2b
Dolayısıyla,
3.2. Birinci Denklemin Sağ Tarafıyla Kıyaslama
Soruya göre bu ifade $k + ab + 4b$’ye eşit:
Burada $k$’yi yalnız bırakmak için benzer terimleri karşılıklı sadeleştirebiliriz. Sol taraftaki ab, sağ taraftaki ab ile aynı olduğu için birbirini götürür (çıkarma yapıldığında aradan çıkar):
Sonra $2b$’yi sağa atmak istersek veya $4b$’yi sola atmak istersek, $k$’yi tek başına bırakmaya çalışırız:
Buradan:
Artık k, a ve b cinsinden bu şekildedir.
4. İkinci Denklemin Kullanımı ( a + b = 2ab )
Elimizde,
ifadesi var. Ayrıca, ikinci denklemden (çarpım sonrası)
biliyoruz. Burada 2ab = a + b eşitliği, özellikle ifademizdeki -2b terimini ve \frac{2}{a} terimini tek bir paydada birleştirdiğimizde işimize yarayacaktır.
4.1. k İfadesini Tek Bir Kesir Haline Dönüştürme
Önce $k$’yi ortak paydada toplayalım, çünkü cevap seçeneklerinin tümü \frac{\text{(ifade)}}{a} biçimindedir. Dolayısıyla
Şimdi -2b ifadesini de \frac{-2ab}{a} diye yazarız (herhangi bir şeyin paydasını a yapabilmek için $b$’yi \frac{ab}{a} şeklinde yazarız, burada kat sayı olarak -2 var):
Yani:
4.2. 2ab Yerine (a + b) Yazma
İkinci denklemden elde ettiğimiz a + b = 2ab sonucuna göre, 2ab yerine (a + b) koyabilir veya bu eşitliği tersine kullanarak -2ab yerine -(a + b) koyabiliriz. Çünkü:
Bu durumda:
Parantezi açar ve çıkarma işlemini yaparsak:
- a + 2 - a - b = (a - a) + (2 - b) = 2 - b.
Dolayısıyla,
Böylece k,
Bu, tam olarak A şıkkındaki ifadedir.
5. Sonuç
Yukarıdaki tüm adımlardan görüleceği gibi, sorudaki koşulları sağlayarak $k$’nin ne olduğunu bulduğumuzda, k = \frac{2 - b}{a} elde ediyoruz. Bu da A seçeneğine tekabül eder. Başka bir deyişle, k aşağıdakilerden (2 − b)/a ifadesine eşittir.
Ayrıntılı Konu Anlatımı ve Kavramlar
Şimdi sorunun çözümünü desteklemek ve olası benzer problemlerle ilişki kurmak adına, ilgili kavramlara biraz daha derinlemesine bakalım. Burada “en küçük ayrıntı”dan “konuların genel mantığı”na kadar değinerek yaklaşık 2.000 kelimeye yakın bir metin sunmuş olacağız.
5.1. Rasyonel Denklemler
Rasyonel denklemler, payında ve paydasında değişkenler bulunan kesirli yapılara sahip denklemlerdir. Örneğin,
gibi bir denklem, rasyonel ifadelere güzel bir örnektir. Bu denklemde dikkat edilmesi gereken en önemli konu, paydadaki değişkenlerin sıfıra eşit olmaması gerekliliğidir (yani a \neq 0, b \neq 0).
5.2. Çarpma-Dağıtma (Expand) Yöntemi
Herhangi iki binomun (iki terimli ifadenin) çarpımı:
$$(x + y)(u + v) = x \cdot u + x \cdot v + y \cdot u + y \cdot v,$$
benzeri dağıtma kuralıyla açılır. Bizim problemimizde:
$$(a + 2)(1 + ab) = a(1 + ab) + 2(1 + ab),$$
yapılmasıyla ilerledik. Bu, temel fakat çok kritik bir adımdır.
5.3. Payda Ortaklaştırma
Bu problemde de gördüğümüz üzere, kesirli ifadeleri daha kolay kıyaslayabilmek için payda ortaklaştırılır. Mesela,
ifadesini tek bir rasyonel ifadede toplamak istediğimizde, $2b$’yi \frac{2ab}{a} şeklinde yazdık. Bu basit yöntem, çok adımda sıkça kullanılır.
5.4. Birinci Dereceden Denklem Manipülasyonu
Birinci dereceden denklem manipülasyonları, aslında a + b = 2ab benzeri eşitliklerle sıkça yapılır. Herhangi bir aşamada, -2ab yerine -(a + b) yazabilmek, işimizi kolaylaştırır. Bu tip manipülasyon, pek çok matematiksel problemde pratiklik sağlar.
5.5. Problemde “K” Sabiti
Soru, (a + 2)(1 + ab)/a = k + ab + 4b ifadesinin yardımıyla bir sabit k çıkarmayı amaçlar. Burada k parametresinin, diğer bilinen terimlerden ayrıştırıldıktan sonra, hangi değere sahip olduğunu tespit ediyoruz. Soruda beş farklı seçenek verilmiş (A, B, C, D, E) ve biz $k$’yi bu seçeneklerden doğru olanla eşleştiriyoruz.
5.6. Sorunun “Neden Önemli?” Boyutu
Böyle bir problem, her ne kadar basit görünse de, aslında cebirsel manipülasyon, payda ortaklaştırma, sıfırdan farklı değişkenlerin önemi, parametre tanımı gibi konularda oldukça didaktik bir örnektir. Öğrencilerin bu tip soruları çözerken şu becerileri güncel tutması gerekir:
-
Denklem genişletme ve sadeleştirme becerisi:
- (a + 2)(1 + ab) = a + a^2b + 2 + 2ab.
-
Payda ayarlama ve tek kesir elde etme becerisi:
- \frac{a + 2}{a} - 2b = \frac{a + 2 - 2ab}{a}.
-
Ek bilgi kullanma:
- a + b = 2ab eşitliği yardımıyla -2ab = - (a + b ) şeklinde dönüştürme yapabilme.
-
Seçenek karşılaştırması:
- Bulduğumuz sonucun, çoktan seçmeli bir testte sunulan seçeneklerle aynı forma getirilmesi.
5.7. Benzer Problemler ve Stratejiler
Bu problem tipinde, “2” gibi sabit bir sayının yerine “n” gibi bir ifade geldiğini veya k + ab + 4b yerine faklı bir lineer kombinasyonun yer aldığını hayal edebiliriz. Dolayısıyla, temel strateji aynıdır:
- Verilen tüm ifadeleri “sade ve açık” hale getirmek.
- Yeni bir denklem varsa, bu denklemi a ve b arasında ek bir bağlantı olarak görmek ve istenen ifadeyi bu bağlantıyı kullanarak basitleştirmek.
Dolayısıyla benzer sorularda da, hangi sayının izole edilmek istendiğini anlayıp, manipülasyonları adım adım yürütmek önemlidir.
5.8. Olası Hata Noktaları
- Dağıtma (expand) sırasında terim atlama: Bu sıklıkla öğrencilerin “(a + 2)(1 + ab)” genişletirken tek veya iki terimi unutmasıyla ortaya çıkabilir.
- Sadeleştirme hataları: Kesirleri ortak paydada toplarken veya benzer terimleri silerken bir eksi işaretinin gözden kaçması gibi basit hatalar yanılgılara sebep olabilir.
- Yanlış seçenekle eşleştirme: Bazen bulunan ifade, seçeneklerin hiçbiriyle görsel olarak hızlıca eşleşmeyebilir. Burada sabırla manipülasyonu sürdürüp, a + b = 2ab gibi ek bilgiden yararlanmak gerekir.
5.9. Bu Denklemin Geometrik Yorumları
Biraz da konuyu farklı perspektifle zenginleştirmek adına, 1/a + 1/b = 2 denkleminin geometrik veya analitik düzlemde bazen hiperbolik eğri türünde bir grafiğe karşılık geldiğini ekleyebiliriz. a ve b “x” ve “y” gibi düşünülürse, xy çarpımına ilişkin sabitin (kısmi) tanımladığı eğrilerin kesişmeleri söz konusu olabilir. Fakat bu problemde asıl amacımız cebirsel bir parametre (k) bulmak olduğu için, geometrik boyuta derinlemesine girmeye çok da gerek yoktur.
5.10. İkinci Dereceye Genişletilebilen Durumlar
Sorularda bazen 1/a + 1/b = \alpha gibi ifadeler, a + b ve ab arasında bağlantılar kurmayı, hatta ileride (a + b)^2 veya ab gibi ifadelerin kullanıldığı polinom denklem sistemlerine gitmeyi gerektirebilir. Mevcut problemde öyle bir gereksinim yok, ancak benzer problemlerle ilgilenen öğrenciler, “Acaba a ve $b$’nin tek bir polinomda kök olduğu durumlar” senaryosunu akılda tutabilir.
5.11. Sonucun Seçeneklerle Uyuşması
Çözüm aşamalarında en kritik noktalardan biri, elde edilen sonucun “test” formatıyla uyuştuğunu kontrol etmektir. Bu soruda beş seçenek vardı:
- (2−b)/a
- (1+b)/a
- (1−b)/a
- (2+b)/a
- b/a
Bizim nihai sonucumuz:
Dolayısıyla A şıkkına birebir uyuyor.
5.12. Matematiksel Yazım Kuralları
Bu sorudaki gibi kesir formlarının doğru yazılması, alt ve üst indislerin doğru konumlanması, \LaTeX (MathJax) türü bir yazım sistemiyle daha profesyonel görünür. Bu sebepten, cevaptaki matematiksel ifadelerin sunumu sıklıkla üniversite düzeyindeki akademik matematik kitaplarında ve dijital öğrenme platformlarında \LaTeX formatında yapılır.
5.13. Örnek Değer Denemesi
Bu soruyu kontrol amaçlı, rastgele a ve b değerleri seçip denemeler de yapabiliriz. Elbette 1/a + 1/b = 2 şartını sağlayacak şekilde bir a ve b seçmek zorundayız. Örneğin:
- a = 1, b = 1 alsak \frac{1}{1} + \frac{1}{1} = 2 gayet sağlanıyor.
- Bu durumda a + b = 1 + 1 = 2, $ab = 1.
- Birinci denklem sol taraf: $\frac{(1 + 2)(1 + 1\cdot1)}{1} = (3)(2) = 6.
- Sağ taraf: $k + ab + 4b = k + 1 + 4 \cdot 1 = k + 5.
- Eşitlik: $6 = k + 5 \implies k = 1.
- Bizim bulduğumuz formülle: k = \frac{2 - b}{a} = \frac{2 - 1}{1} = 1.
- Bu da A şıkkı ifadesiyle doğrudan uyumlu olduğunu onaylar.
Bu tek bir test senaryosu elbette tüm problem için garanti teşkil etmez, ancak formülün doğru işlediğini göstermesi açısından değerlidir.
Adım Adım Özet Tablosu
Aşağıda, çözüme ulaşmak için her adımdaki işlem ve elde edilen sonucu özet bir tabloda sunuyoruz:
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Denklem (1) genişletme | (a + 2)(1 + ab) ifadesini dağıtma yöntemiyle açıyoruz: a(1 + ab) + 2(1 + ab) = a + a^2b + 2 + 2ab. |
a + a^2b + 2 + 2ab. |
| 2. Payda bölme | Elde edilen toplamı $a$’ya bölüyoruz: \frac{a + a^2b + 2 + 2ab}{a} = \frac{a}{a} + \frac{a^2b}{a} + \frac{2}{a} + \frac{2ab}{a}. |
1 + ab + \frac{2}{a} + 2b. |
| 3. Denklem (1) ile eşleştirme | 1 + ab + \frac{2}{a} + 2b = k + ab + 4b. | k = 1 + \frac{2}{a} + 2b - 4b. |
| 4. Sadeleştirme | k = 1 + \frac{2}{a} - 2b. | k bu şekilde yazıldı. |
| 5. Tek kesir altında birleştirme | k = \frac{a + 2}{a} - 2b = \frac{a + 2 - 2ab}{a}. | \frac{(a + 2) - 2ab}{a}. |
| 6. İkinci denklem (2) kullanma | a + b = 2ab \implies -2ab = -(a + b). | a + 2 - 2ab = (a + 2) - (a + b) = 2 - b. |
| 7. Nihai ifade | \frac{a + 2 - 2ab}{a} = \frac{2 - b}{a}. | k = \frac{2 - b}{a}. |
| 8. Seçenek karşılaştırması | \frac{2 - b}{a} ifadesi seçeneklerde A şıkkında mevcuttur. | Doğru yanıt: (2 - b)/a (A şıkkı). |
Sonuç ve Kısa Özet
Bu problemde, öncelikle birinci denklemi genişleterek ve sadeleştirerek $k$’yi a ve b cinsinden ifade ettik. Ardından, ikinci denklemdeki 1/a + 1/b = 2 koşulunu, çarpma yoluyla a + b = 2ab şekline dönüştürüp manipülasyonlarda kullandık. Sistematik olarak yaptığımız bu adımlar sonunda, k = \frac{2 - b}{a} sonucunu bulduk. Çoktan seçmeli test formatında, bu ifade A seçeneğine karşılık gelmektedir. Dolayısıyla sorunun cevabı A) (2 - b)/a şeklindedir.